Вопрос 21. Линейчатые развертываемые поверхности

Характерным признаком линейчатых развертываемых поверхностей является то, что их прямолинейные образующие пересекаются. При этом пересечение может происходить как в собственной (S), так и в несобственной (S) точках. К рассматриваемой группе относятся:

• поверхность с ребром возврата;

• поверхность коническая;

• поверхность цилиндрическая.

Поверхность с ребром возврата

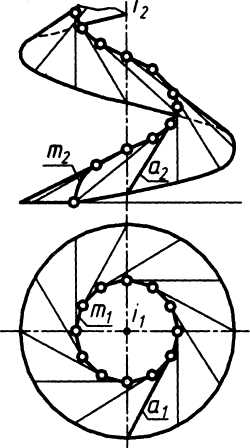
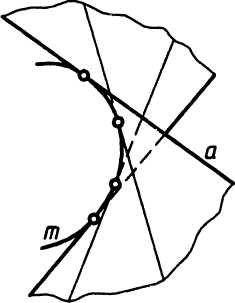
Поверхность с ребром возврата в общем случае образуется непре­рывным перемещением прямолинейной образующей (а), касающейся про­странственной кривой (m) - направляющей (рис. 1 а). Кривая m называ­ется ребром возврата торса.

Торсовая поверхность состоит из двух полостей, линией раздела ко­торых является ребро возврата. Ребро возврата полностью задает торс и является геометрической частью определителя поверхности. Алгоритмиче­ской частью служит условие касания образующих к ребру возврата.

Определитель имеет вид Ώ (a, m)[a U т].

На эпюре Монжа любая неограниченная торсовая поверхность зада­ется только проекциями ребра возврата (т1 и m2). При этом каркас поверх­ности можно составить из семейства прямолинейных образующих, каса­тельных к этому ребру. Так, на рис. 1б проекциями образующей (а) яв­ляются касательные а₁ и а₂ к проекциям т₁ и т₂ ребра возврата m, прове­денные через проекции A₁ и A₂ случайной точки А этого ребра.

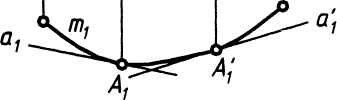
а) рис. 1 б)

Наиболее широкое применение в инженерной практике нашел част­ный вид торсовой поверхности - винтовой торс, у которой ребром возврата служит цилиндрическая винтовая линия. Если ось винтовой линии распо­ложить перпендикулярно к П₁ то образованная поверхность представит собой поверхность одинакового ската (по отношению к П₁), т.к. все каса­тельные к винтовой линии пересекают плоскость П₁ под одним и тем же углом. Чертеж отсека такой поверхности показан на рис. 2.

В процессе решения многих задач приходится задавать точки на по­верхности изучаемых предметов.

В некоторых случаях, намечая проекции точки на поверхности, не­обходимо указывать видимость данной точки на той или иной проекции. Такое указание делают путем заключения в скобки невидимой проекции точки. На данной (как и любой торсовой) поверхности точки могут быть построены при помощи проходящих через них прямолинейных образую­щих.

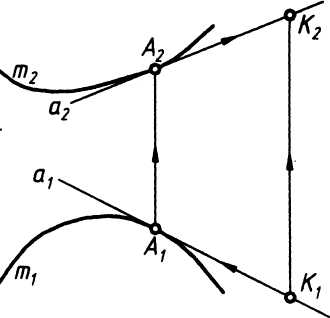
Так, на рис. 3 показано построение фронтальной проекции К₂ точ­ки К, лежащей на поверхности с ребром возврата, по заданной горизон­тальной К₁. Для этого через точку К₁ проведена касательная а₁ к проекции m₁ направляющей m. Далее через фронтальную проекцию А₂ полученной точки А на ребре возврата т проведена фронтальная проекция а₂ касатель­ной а, на которой расположена точка К. Линия связи, проведенная из К₁ определяет искомую проекцию К₂.

В некоторых случаях недостающую проекцию точки строят при по­мощи произвольной секущей плоскости, с расчетом, что точка должна быть в этой плоскости.

Рис. 2 Рис. 3