Всем удачного экзамена, спасибо за участи в подготовке ответов по начерталке!

P.S. 19 и 20 вопросы спрашивать не будут так сказал Экзаменатор!!!!!

Билет №1

Метод проекций

Прямой задачей начертательной геометрии является задача построения чертежа, т.е. изображения предмета на плоскости и изучение способов этого построения.

Под проекцией предмета на плоскость подразумевают его изображение, отброшенное на эту плоскость с помощью воображаемых проецирующих лучей.

 Для отображения точек оригинала на чертеже применяют операцию проецирования. Имеется плоскость проецирования (ее иногда называют картинная плоскость), на которой получается изображение оригинала - точки А. Операция проецирования заключается в проведении через точку А прямой, которая называется проецирующей.

Центральное и параллельное проецирование

В зависимости от положения проецирующих лучей проецирование может быть либо центральным (коническим), либо параллельным (цилиндрическим).  Наиболее общий случай получения проекций пространственных фигур - это центральное проецирование.  В этом случае проецирующие лучи выходят из одной точки - центра проецирования S, который находится на конечном расстоянии от плоскости проекций П₁.

 Если центр проекций при центральном аппарате проецирования перенести в бесконечность, то проецирующие лучи можно считать параллельными. Отсюда аппарат параллельного проецирования состоит из плоскости проекций П и направления Р. При центральном проецировании проецирующие лучи выходят из одной точки, а при параллельном проецировании - параллельны между собой.  В зависимости от направления проецирующих лучей параллельное проецирование может быть косоугольным, когда проецирующие лучи наклонены к плоскости проекций, и прямоугольным (ортогональным), когда проецирующие лучи перпендикулярны к плоскости проекций.

Свойства параллельного проецирования

 Проекцией точки является точка.

 Проекцией линии является линия.

 Проекцией прямой в общем случае является прямая. (Если прямая совпадает с проецирующим лучом, то её проекцией является точка).

 Если точка принадлежит линии, то проекция точки принадлежит проекции линии.

 Точка пересечения линий проецируется в точку пересечения проекций этих линий.

 В общем случае плоский многогранник проецируется в многогранник с тем же числом вершин.

• Проекции параллельных прямых параллельны.

• Если точка делит длину отрезка в отношении m:n, то проекция этой точки делит длину проекции отрезка в том же отношении.

• Плоская фигура, параллельная плоскости проекций, проецируется без искажения.

Проекция точки

 По отношению к плоскостям проекций точка может занимать общее положение, т. е. ни принадлежать ни одной из плоскостей проекций, и частное положение - находиться на одной из этих плоскостей, сразу на двух плоскостях проекций и одновременно на трёх плоскостях.

Конкурирующие точки

Конкурирующими называют точки лежащие на одном проецирующем луче. Бывают фронтально, горизонтально, профильно-конкурирующие точки.

Билет №2

Сущность ортогонального проецирования

Сущность ортогонального проецирования заключается в том что бы получить трехмерное изображение детали на плоскостях проекции.

Метод ортогональных проекций обладает рядом преимуществ. Наиболее важных из них является возможность при определенных условиях сохранить на проекциях формы и размеры проецируемой фигуры.

Основные элементы ортогонального проецирования это 3-х мерное пространство(x,y,z)->2-х мернаю плоскость(плоскость xy,yz,zx)

координата точки есть расстояние от точки до ближайшей плоскости проекции. минимальное количество проекций две, т.к. есть все три координаты

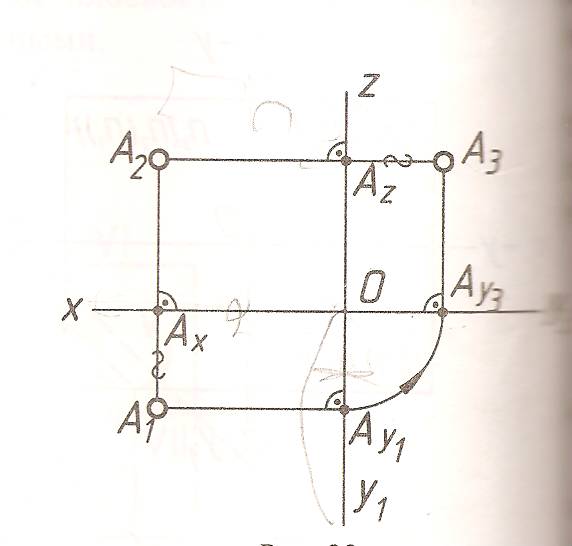
комплексный чертеж смотри эпюр Монжа

Билет №3

Сущность способа замены плоскостей проекции заключается в том, что одну из плоскостей проекций ортогональной системы заменяют на новую, которая в совокупности с оставшейся плоскостью образуют другую ортогональную систему плоскостей проекций. При этом новую плоскость вводят так, чтобы относительно нее проецируемый геометрический образ занял частное положение.

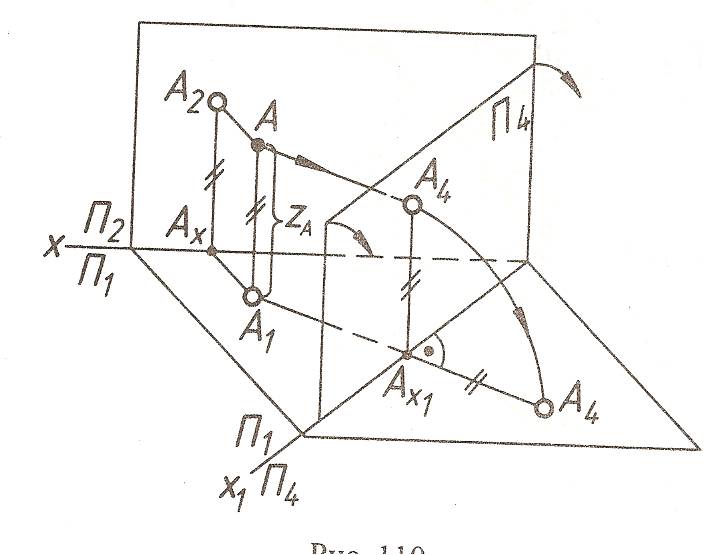
Проекция точки на дополнительной плоскости проекции.

Плоскость П2 заменяем на новую плоскость П4, расположенную под углом к П2 не равным 90 градусов. При этом П4 будет перпендикулярна горизонтальной плоскости проекций П1 и пересекать ее по оси Х1. Точка ортогонально проецируется на П4, образуя новую проекцию точки- А4. Таким образом, будем иметь две системы плоскостей проекции старую и новую с общей плоскостью П1. Эти же рассуждения сохраняются и при построение новой проекции точки на эпюре, полученном после совмещения плоскостей П1 и П4 м плоскостью П2.

Билет №4

Комплексный чертёж линии представляет собой совокупность проекций точек этой линии на две или три плоскости проекций. На комплексном чертеже необходимо установить связь между проекциями точек. В этом случае линия будет определена однозначно.

Так как две точки однозначно определяют положение прямой в пространстве, то нам достаточно задать на комплексном чертеже проекции двух точек, принадлежащих прямой и попарно соединить их первые, вторые и третьи проекции.

 

По расположению относительно плоскостей проекций прямые могут быть общего и частного положений.

 Прямой общего положения называется прямая, не параллельная ни одной из плоскостей проекций.

Прямая частного положения (или прямая уровня) - прямая, параллельная хотя бы одной из плоскостей проекций.

1.Прямая, параллельная горизонтальной плоскости проекций, называется горизонталью - h. На горизонтальную плоскость проекций горизонталь проецируется в натуральную величину.

2.Прямая, параллельная фронтальной плоскости проекций, называется фронталью - v. На фронтальную плоскость проекций фронталь проецируется в натуральную величину.

3. Прямая, параллельная профильной плоскости проекций, называется профильной прямой - w. На профильную плоскость проекций профильная прямая проецируется в натуральную величину.

 Прямая называется проецирующей, если она перпендикулярна одной из плоскостей проекций. Одна из проекций такой прямой есть точка. Эта проекция называется главной или вырожденной. Все точки проецирующей прямой являются конкурирующими.

1. Горизонтально проецирующая прямая - прямая 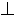горизонтальной плоскости проекций. Горизонтальной проекцией такой прямой является точка, а фронтальная и профильная проекции || оси z.

2. Фронтально проецирующая прямая - прямая фронтальной плоскости проекций. Фронтальной проекцией такой прямой является точка, а горизонтальная и профильная проекции || оси y.

3. Профильно проецирующая прямая - прямая профильной плоскости проекций. Профильной проекцией такой прямой является точка, а горизонтальная и фронтальная проекции || оси x.

 Если точка С лежит на прямой АВ, то, на основании свойства проекций при параллельном проецировании, её проекции лежат на одноимённых проекциях этой прямой и на одной линии связи.

Прямая общего положения пересекает плоскости проекций в 2-х точках – эти точки называют следами прямой. Прямую общего положения можно задать следами. Каждый след задается двумя координатами (параметрами), следовательно прямая в пространстве определена 4 параметрами.

Билет №5

Определение натур. Велечины и углов

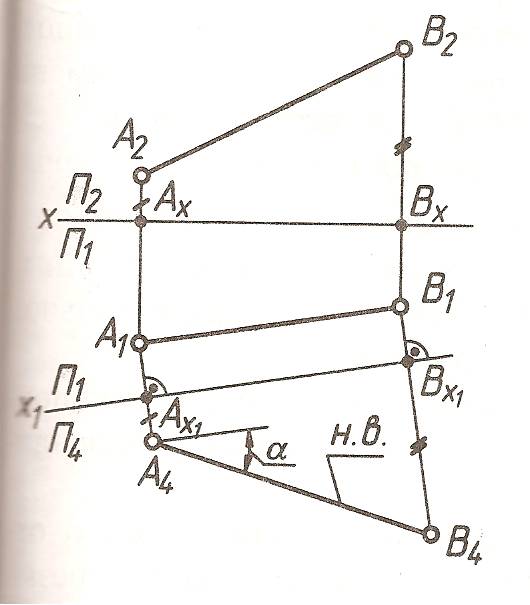
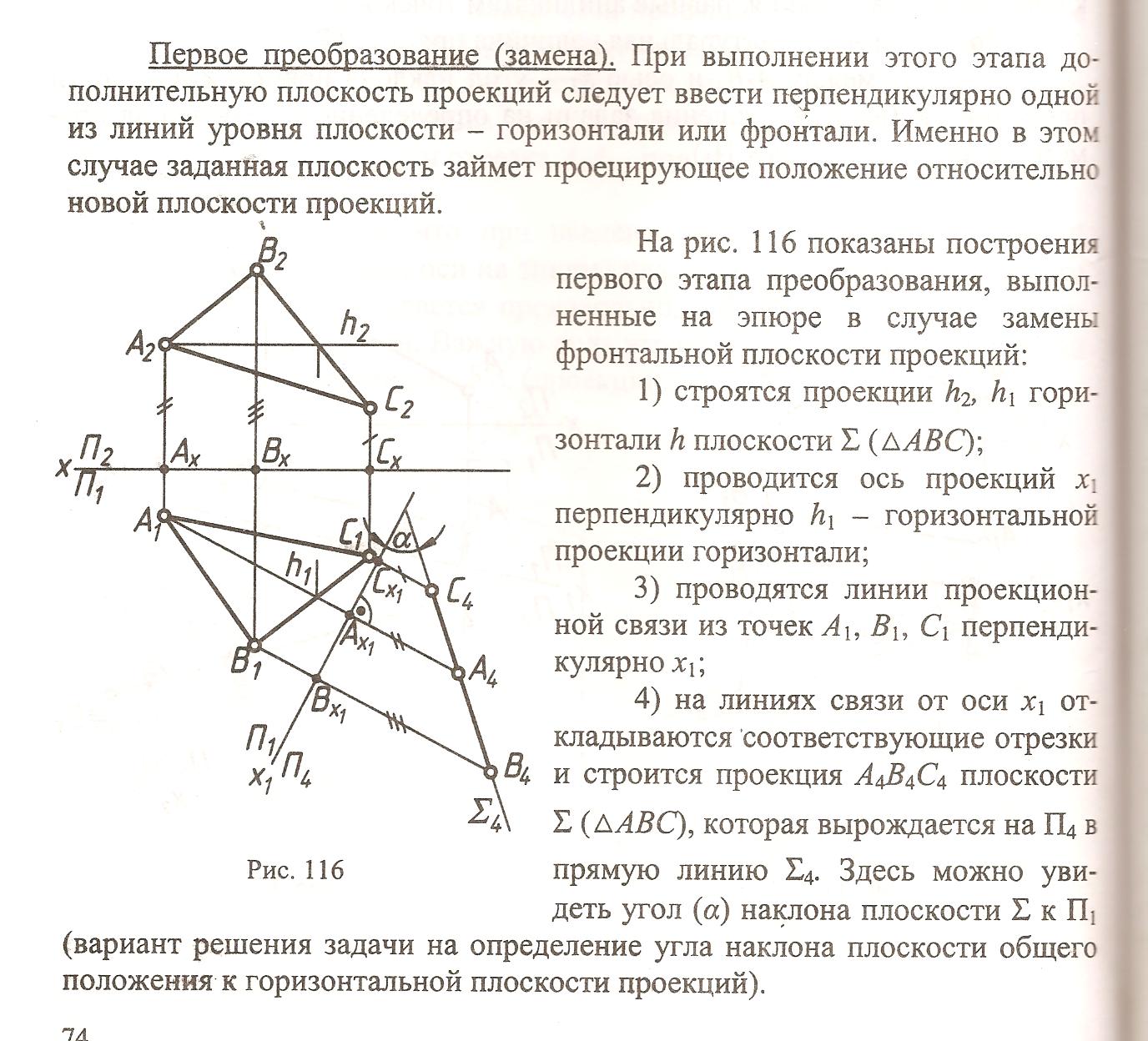
Допустим есть прямая общего положения АВ, сначала приведем ее к положению уровня. Для этого заменим одну из плоскостей проекции системы П1П2 , например П2, на плоскость П4, которая будет параллельна АВ и перпендикулярна П1. на П4 прямая проецируется в натуральную величину

Необходимые построения на эпюре, выполняем при замене плоскости проекции

1. Проводится ось Х1 параллельно горизонтальной проекции прямой А1В1

2. Проводится линия проекционной связи из А1 и В1 перпендикулярно оси Х1

3. Для построения проекции А4В4 на линиях связи от новой оси Х1 откладываются расстояния, равные аппликатам точек А и В

Проекция А4 и В4 натуральная величина прямой АВ

Угол между А4В4 и осью Х1- угол наклона прямой к плоскости проекций П1

Способ прямоугольного треугольника заключается в том что бы перенести н. в. и достроить до треугольника.

Сущность способа замены плоскостей проекции заключается в том, что одну из плоскостей проекций ортогональной системы заменяют на новую, которая в совокупности с оставшейся плоскостью образуют другую ортогональную систему плоскостей проекций. При этом новую плоскость вводят так, чтобы относительно нее проецируемый геометрический образ занял частное положение.

БИЛЕТ№6

В пространстве две прямые могут либо пересекаться, либо быть параллельными, либо быть скрещенными.

Прямые линии, имеющие общую точку, называются пересекающимися.

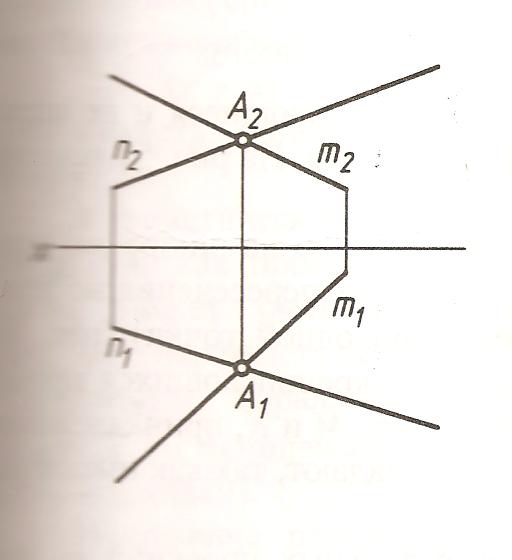
Свойство: если прямые пересекаются, то точки пересечения их одноимённых проекций находятся на одной линии связи.

Прямые линии, пересекающиеся в несобственной точке, называются параллельными.

Свойство: параллельность отрезков прямых сохраняется в проекциях.  Обратное свойство: если проекции прямых на всех плоскостях проекций параллельны, то прямые параллельны.

Прямые, не пересекающиеся и не параллельные между собой, называются скрещивающимися.

Свойство: на чертеже одноименные проекции прямых, взятые отдельно, имеют признаки пересекающихся или параллельных прямых.

БИЛЕТ№7

БИЛЕТ №8

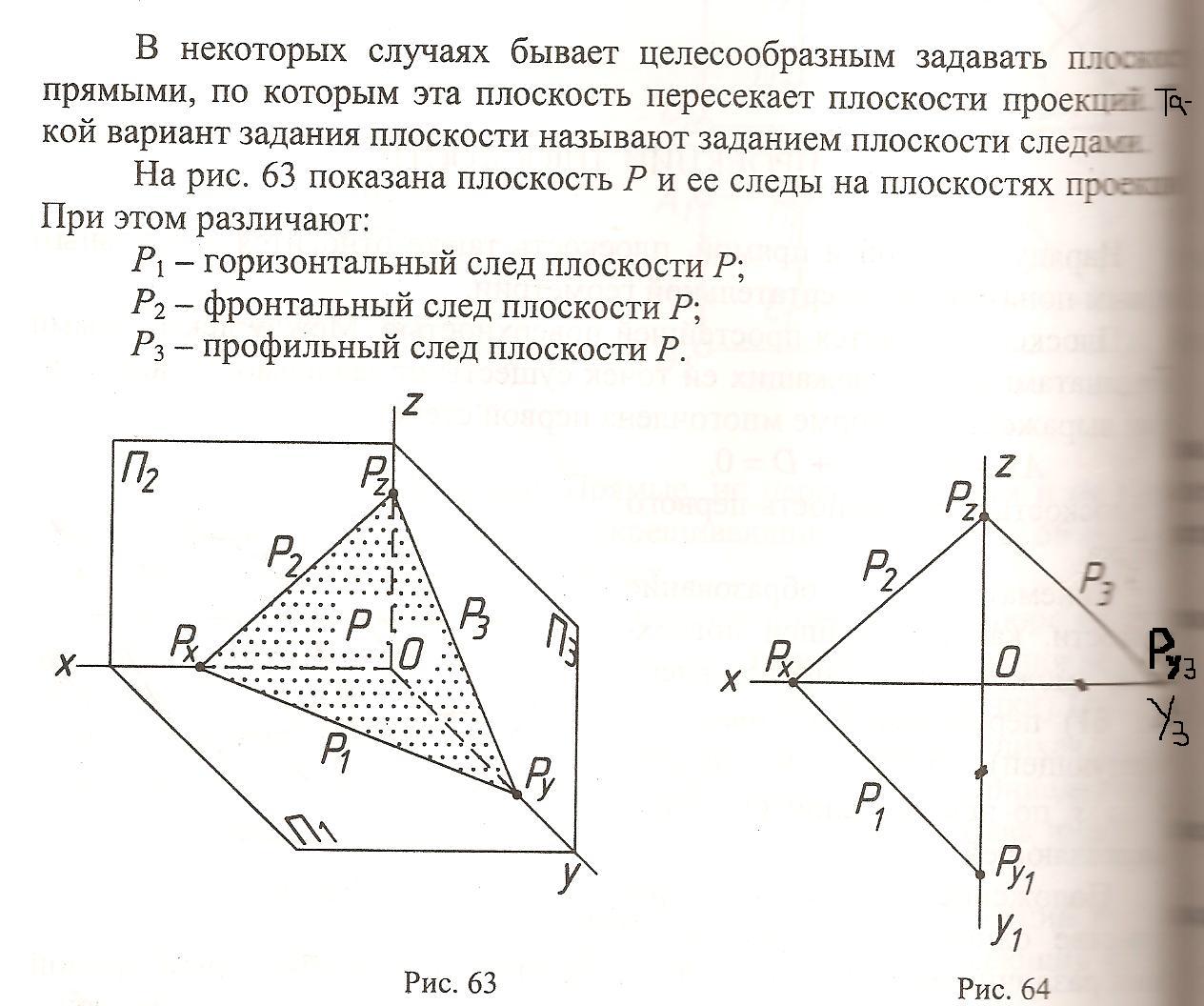
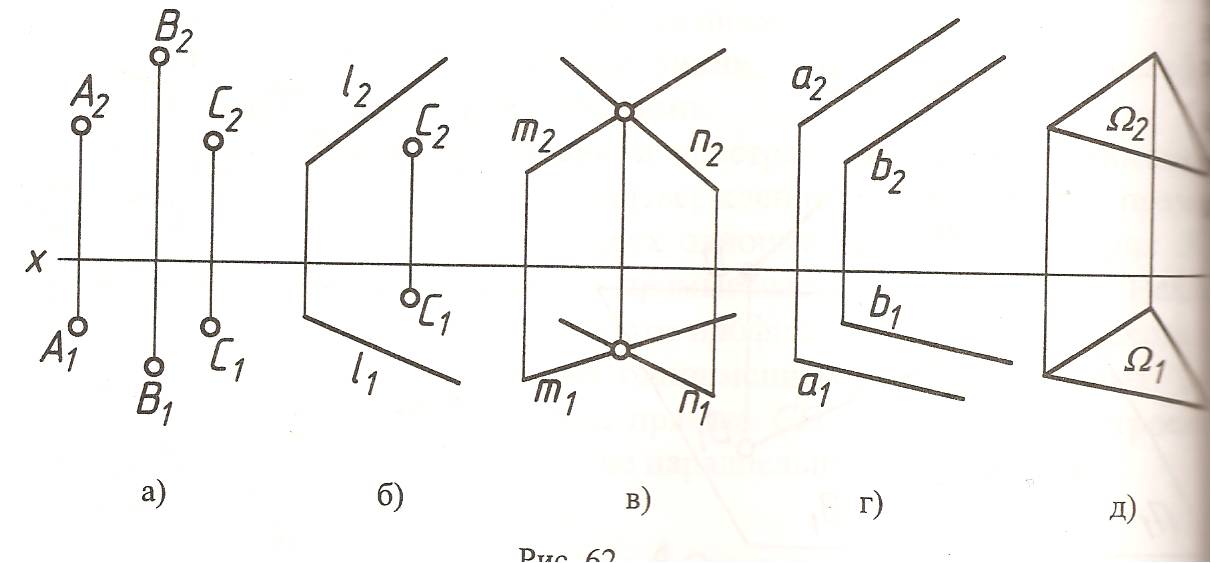
Плоскость- простейшая поверхность, поверхность второго порядка.

Плоскость можно задать

• Тремя точками, не лежащими на одной прямой; (а)

• Прямой и точкой, ей не принадлежащей; (б)

• Двумя пересекающимися прямыми; (в,г)

• Двумя параллельными прямыми. (д)

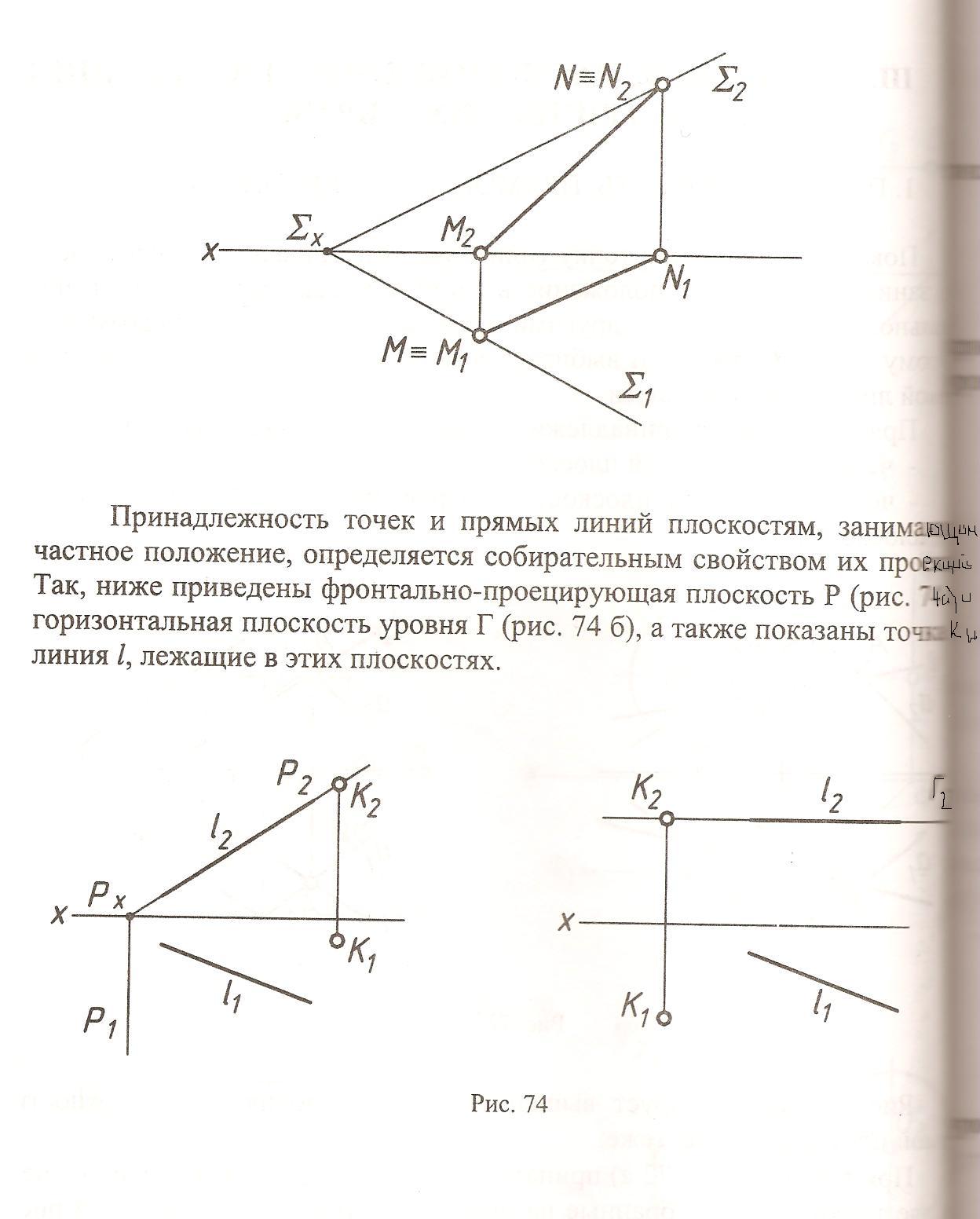
Билет №9

Плоскость относительно плоскостей проекций может занимать общее и частное положение:

Плоскость общего положения - плоскость не перпендикулярная ни к одной из плоскостей проекций.

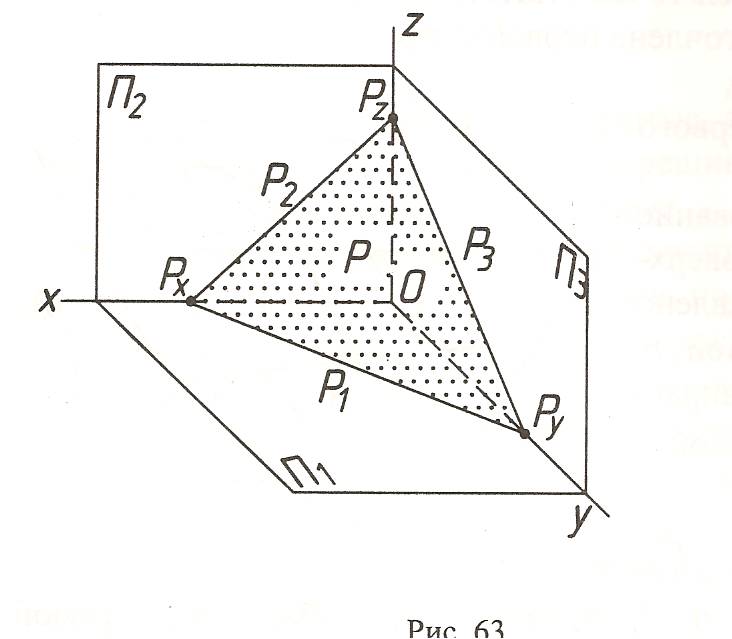
Плоскость частного положения - плоскость проходящая через проецирующие прямые, т.е. перпендикулярная к одной или одновременно к двум основным плоскостям проекций. Если плоскость перпендикулярна только к одной плоскости проекций, то она называется проецирующей плоскостью. Существует три вида проецирующих плоскостей:

1. Горизонтально-проецирующая плоскость - перпендикулярна к П₁. И поэтому проецируется на нее как прямая.

2. Фронтально-проецирующая плоскость - перпендикулярна к П₂. И поэтому проецируется на нее как прямая.

3. Профильно-проецирующая плоскость - перпендикулярна к П₃. И поэтому проецируется на нее как прямая. На обычном ортогональном чертеже, когда плоскость П₃ не используется, профильно-проецирующая плоскость выглядит как плоскость общего положения.

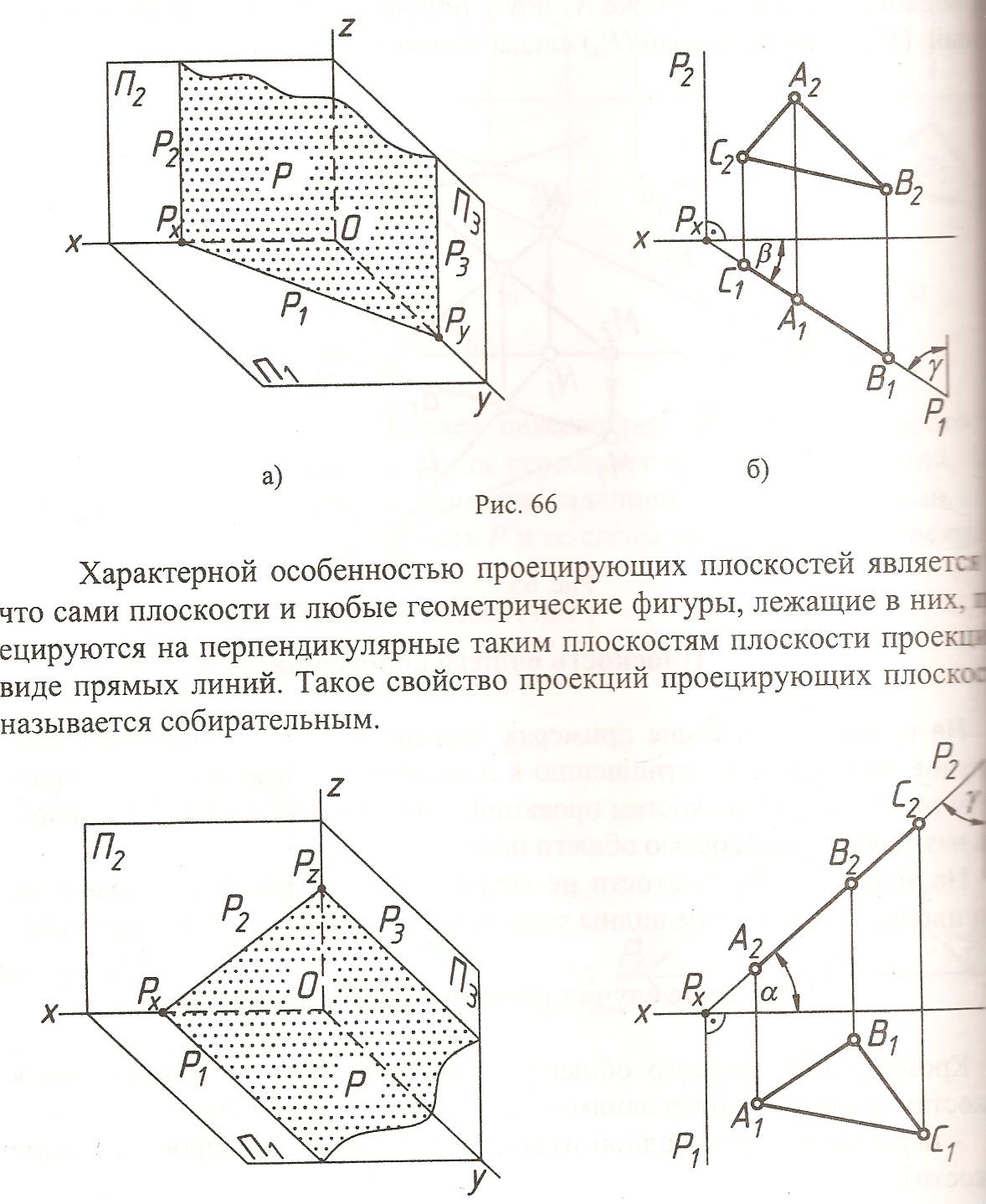
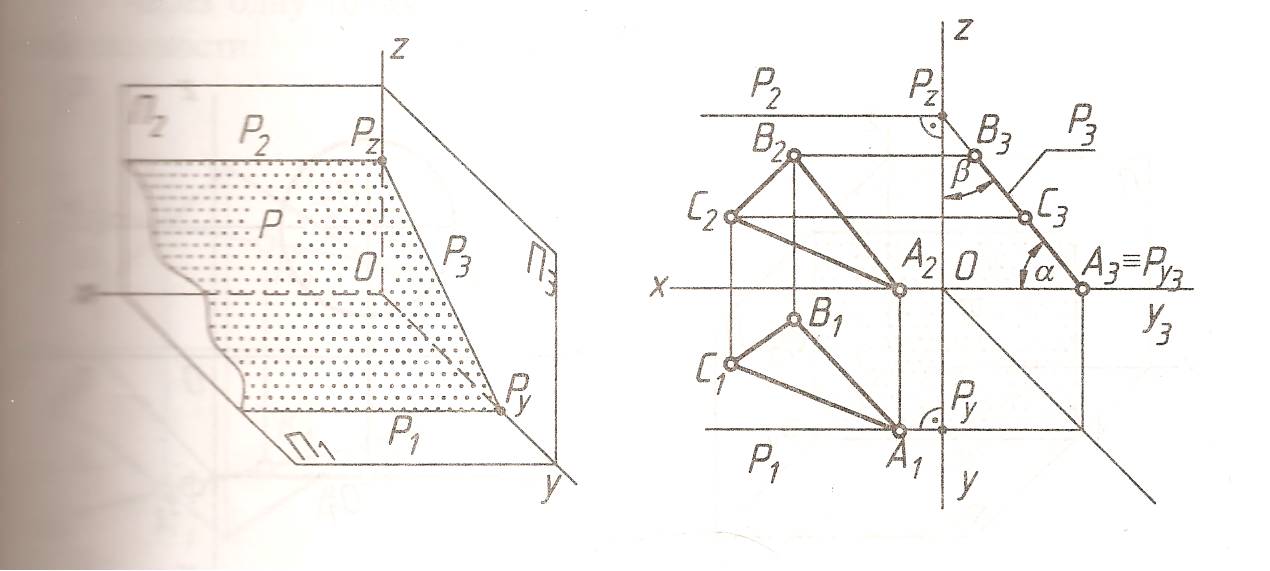
Если плоскость перпендикулярна к двум плоскостям проекций, то она называется плоскостью уровня. Следовательно, плоскость уровня всегда параллельна одной из плоскостей проекций. Существует три вида плоскостей уровня:

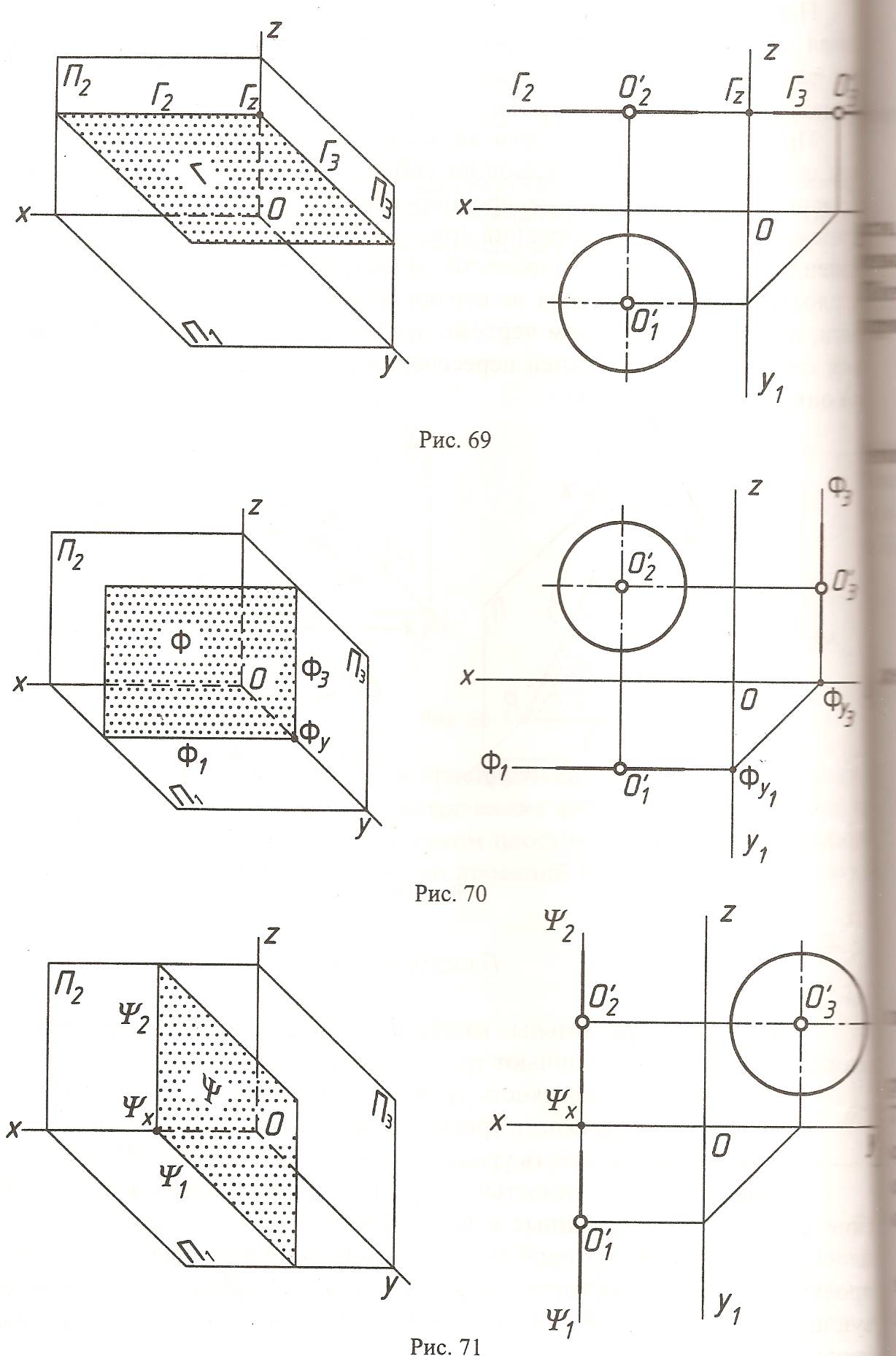
1. Горизонтальная плоскость уровня - || П₁.

2. Фронтальная плоскость уровня - || П₂.

3. Профильная плоскость уровня - || П₃.

 Прямые уровня - это прямые, принадлежащие плоскости и параллельные какай - либо плоскости проекций. Эти прямые называют прямыми уровня, так как они принадлежат плоскости уровня. Существует три вида прямых уровня:

• h - горизонталь плоскости - прямая принадлежащая данной плоскости и || П₁;

• f - фронталь плоскости - прямая принадлежащая данной плоскости и || П₂;

• w - профильная прямая плоскости - прямая принадлежащая данной плоскости и || П₃.

 Прямая, принадлежащая плоскости и к горизонтали, фронтали или профильной прямой, называется линией наибольшего наклона плоскости к плоскости проекций П₁, П₂ или П₃. Линию наибольшего наклона к плоскости проекций П₁ называют линией наибольшего ската.

Прямые уровня и линии наибольшего наклона плоскости к плоскости проекций называют главными линиями плоскости

Билет №10

Вопрос 11

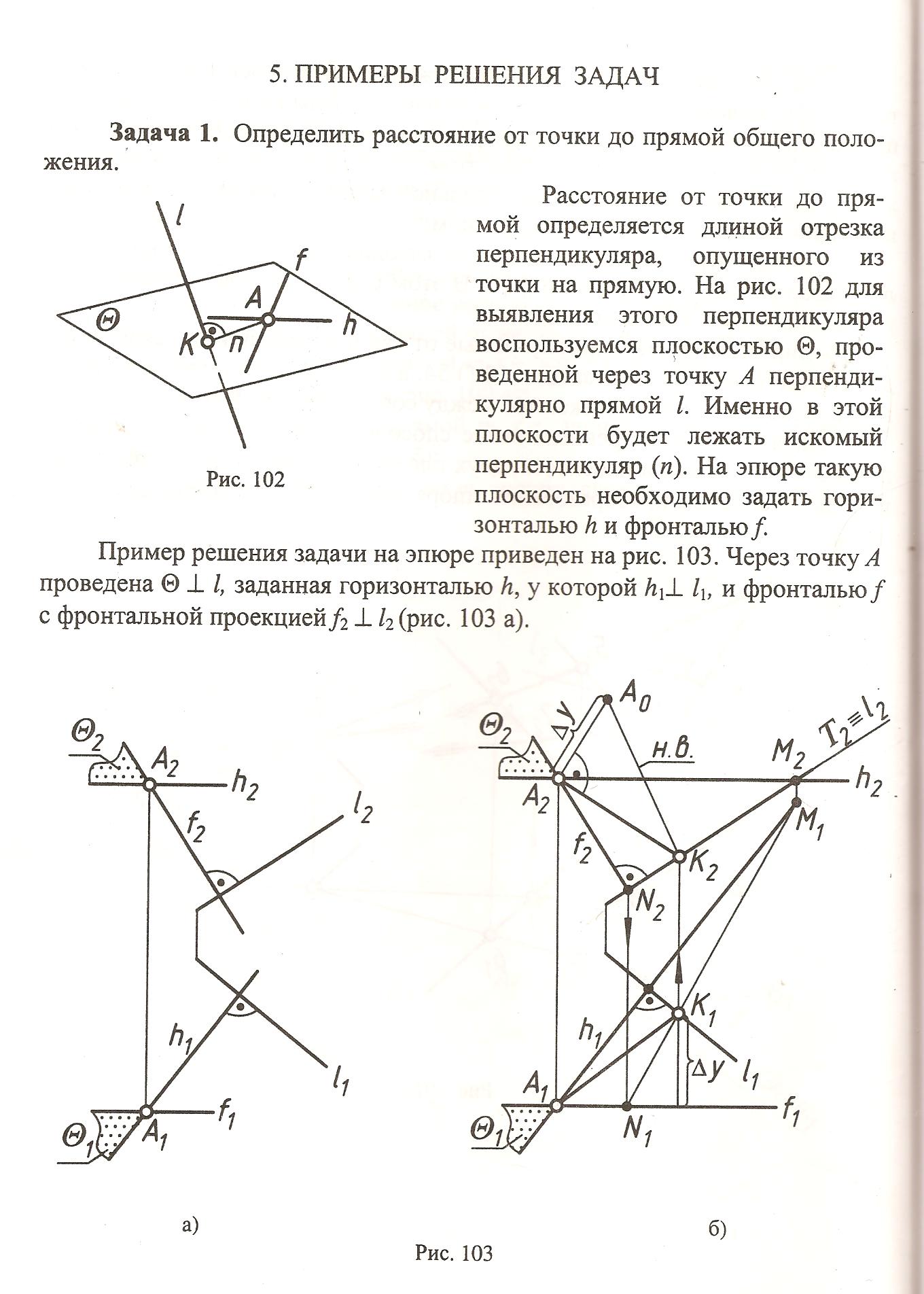
Взаимное положение прямой и плоскости: прямая, параллельная плоскости.

Прямая параллельна плоскости, если она параллельна какой-либо прямой этой плоскости. Через заданную точку пространства можно провести бесконечное множество прямых линий, параллельных заданной плоскости.

Для получения единственного решение требуется задать дополнительное условие – определить прямую, принадлежащую данной плоскости. Так, на рисунке показана прямая АВ параллельная плоскости, так как она параллельна прямой А’В’, лежащей в этой плоскости.

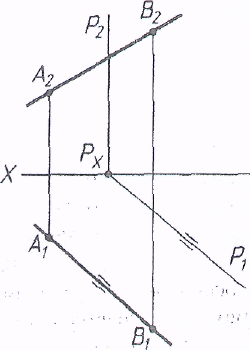
Если плоскость занимает частное по­ложение, то признаком параллельности прямой и плоскости на чертеже будет служить парал­лельность проекции прямой вырожденной проекции плоскости.

Вопрос 12

Взаимное положение прямой и плоскости: прямая, пересекающая плоскость. Алгоритм определения точки пересечения прямой и плоскости частного и общего положения. Определение видимости прямой с помощью конкурирующих точек.

Признаком пересечения прямой и плоскости является наличие точки, одновременно принадлежащей прямой и плоскости.

Если плоскость занимает частное положение, то точкой пе­ресечения прямой с плоскостью будет точка пересечения проекции прямой с вырожденной проекцией плоскости.

Здесь искомой является точка К, горизонтальная проекция которой определяется при пересечении следа Р1 плоскости Р с горизонтальной проекцией прямой l

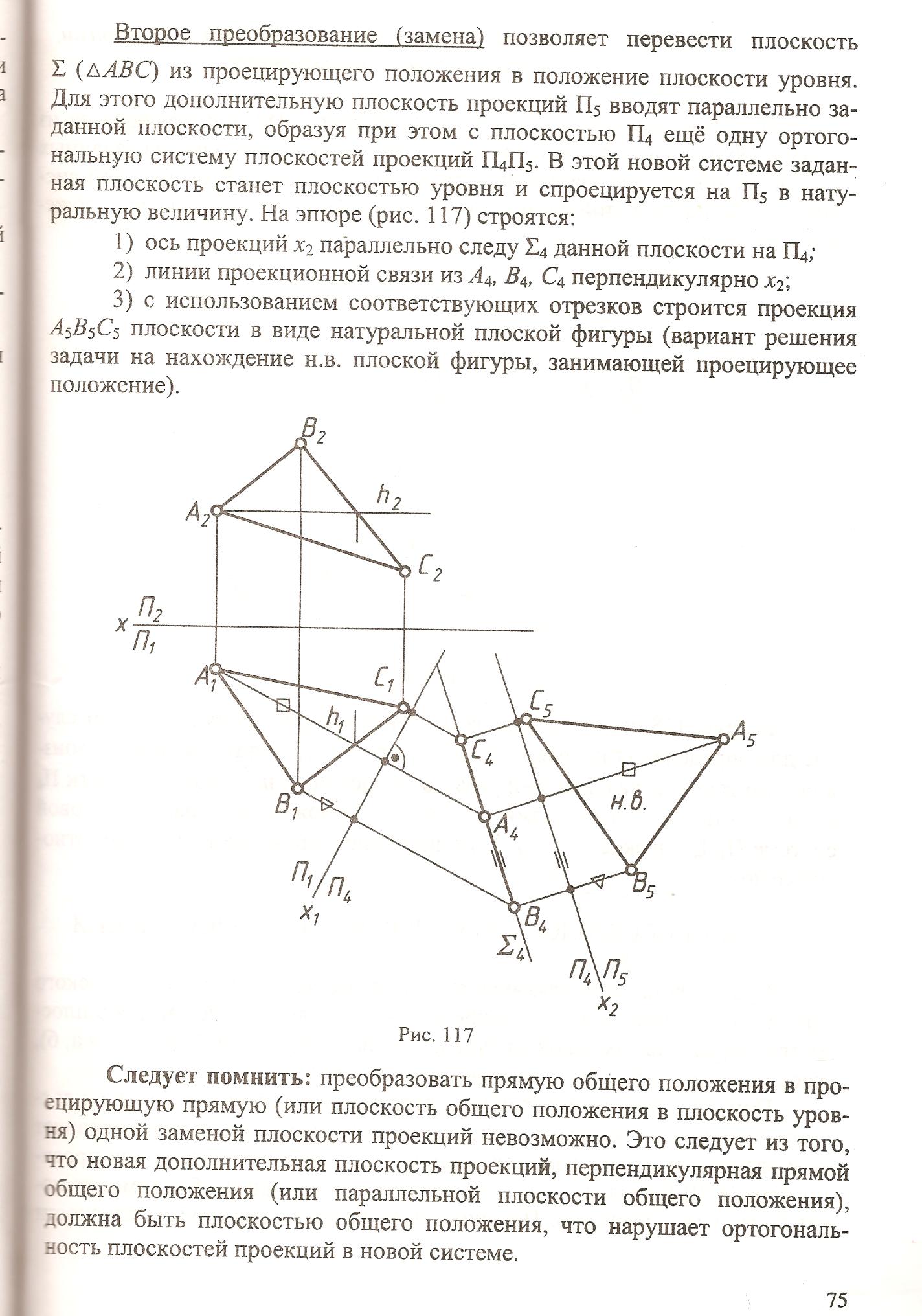
Если плоскость за­нимает общее поло­жение, то нахождение точек пересечения без дополнительных построений невозможно. Точка на­ходится способом вспо­могательных секущих плоскостей. Суть способа заключается в том, что в системе плоскостей проекций с заданными геометрическими образами вводятся дополнительные вспомогательные секущие плоскости. Такие плоскости пересекают заданные геометрические образы и позволяют с помощью ряда построений выявить общие для обоих образов точки. В качестве секущих удобно использовать плоскости частного положения.

А лгоритм определения точки пересечения прямой и плоскости общего положения.

1. через заданную прямую проводят вспомогательную секущую плоскость

2. строят линию пересечения двух плоскостей – секущей и заданной

3. находят общую точку построенной линии пересечения с заданной прямой

4. определяют видимость прямой относительно плоскости

Определение видимости с помощью конкурирующих точек.

Для определения видимости используют пару конкурирующих точек. Видимость на горизонтальной плоскости определяется с помощью горизонтально-конкурирующих

Вопрос 13

Взаимное положение двух плоскостей: взаимно параллельные плоскости.

Плоскости взаим­но параллельны,

если две пересекающиеся прямые

одной плоско­сти параллельны двум

пересекающимся пря­мым другой.

а!! а', b!! b'=>∑!!∑°

Это могут быть как прямые плоскости так

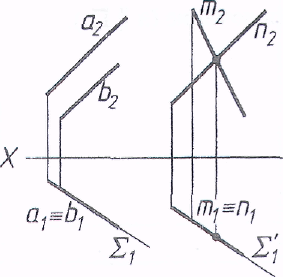и следы плоскости

При плоскостях частного положения

признаком параллельности является

параллельность их вырож­денных проекций.