9. Основные количественные соотношения пассивной диффузии веществ через биологические мембраны.
При переносе веществ через биологические мембраны сопротивлением являются мембраны и примембранные слои.
-диффузия
вещества через мембрану;
-
установившийся поток
(1)
(
);
Вывод формулы (1):
;
;
lH2O=0,3…1мкм
lH2O=(100…300)lM
→вязкость мембраны в 10…100 раз выше вязкости воды.
,
Коэффициент распределения вещества играет определяющую роль;
(→определяющую роль играет гидрофобность).
Примембранные слои воды практически не влияют на общую проницаемость ионов.
Для ионов и гидрофильных веществ основной барьер – это мембрана {200…500мкм – основное препятствие}.
10. Ионные равновесия: потенциал Нернста и потенциал Доннана, - механизмы формирования.
Равновесное состояние. Уравнение Нернста.
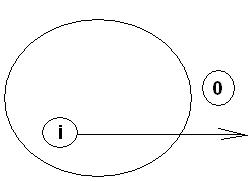
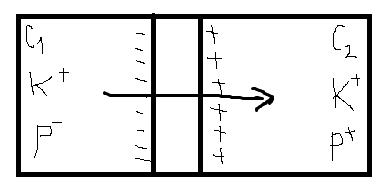
Механизмы электрогенеза в клетках.
1) Если мембрана проницаема только для одного вида ионов и концентрации этих ионов по обе стороны мембраны не равны, то возникает трансмембранная разность потенциалов, при которой нет преобладающего перехода ионов через мембрану в каком-то одном напревлении, так что система находится в равновесии.
Ф=0 – в равновесном состоянии.
,
2) Доннановское равновесие и Доннановский потенциал – устанавливается между клеткой и окружающей средой всегда, когда мембрана хорошо проницаема для органических ионов, но непроницаема для белков и других крупных органических ионов (нарушены механизмы избирательной проницаемости).
Характерен для клеток с ослабленным метаболизмом и мертвых клеток.
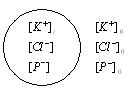n=10…20
(количество единичных зарядов).
Условия электронейтральности:
(1)
клеточная среда;
(2)
внеклеточная среда.
(3).
Движение K и Cl через мембрану прекратится, когда система достигнет равновесия, при котором потенциал Нернста для К и Cl должен быть одинаковым.
(
)
,
(z = +1);
,
(z = -1).
(4) – соотношение Доннана для всех типов
неорганических ионов, для которых
проницаема мембрана.
(
)
(5)
(6)
(7)
n=10…20, n=15
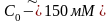и
выше
При х=0,1 δ=0,03%
- Доннановская
равновесная разность потенциалов.
n=15,
,
,
T=310K
При
малых х:
11. Электродиффузионная теория транспорта ионов через мембраны; уравнение Теорелла; уравнение электродиффузии Нернста-Планка; решение дифференциального уравнения Нернста-Планка;
Уравнение Гольдмана для потока ионов через мембрану.
Потоки веществ в результате диффузии и электродиффузии.
Уравнение Теорелла.
Электродиффузионное уравнение Нернста-Планка
↑основное уравнение электродиффузии
Уравнение Нернста-Планка описывает пассивный перенос частиц в условиях существования градиентов концентраций вещества и электрического потенциала в растворе или однородной напряжен. мембране. (наличие зарядов внутри самой мембраны)
Причины переноса вещества при пассивном транспорте: градиент концентрации dc/dx и градиент электрического потенциала dφ/dx. Знаки минусов перед градиентами показывают, что градиент концентрации вызывает перенос вещества от места с большей концентрацией к местам с его меньшей концентрацией; а градиент эл.потенциала
вызывает перенос положительных зарядов от мест с большим к местам с меньшим потенциалом.
Решение уравнения Нернста-Планка в приближении Гольдмана
Электродиффузионное уравнение Нернста-Планка можно решить с использованием
приближения Гольдмана,
при котором напряженность электрического поля внутри мембраны считается постоянной
при всех 0 < x
< l
.
Постоянство поля позволяет произвести
замену:
;
Заметим, что поток мы считаем постоянным при всех х (принцип неразрывности потока),
что верно для стационарного состояния системы.
Заменим DK/l
коэффициентом
проницаемости P:
(ур-е
Больцмана)
Величина ψ
называется
внутримембранным скачком потенциала
↑ Уравнение Гольдмана.
Уравнение Гольдмана позволяет вычислить величину пассивного тока ионов, если известны их концентрации по обе стороны мембраны, трансмембранная разность потенциалов и коэф-т проницаемости.