19. Теорема Ферма

Т.: Пусть ф-ия y=f(x) определена на некотором интервале (a,b) и во внутр.точке этого интервала принимает наибольш. или наименш. знач. Если в этой точке сущ. Конечная производная, то она равна 0. Геометрич. реализация т.Ферма заключ. в том, что если в точке c (a,b) ф-ия y=f(x) приним. наибольш. или наименш. знач., то касательная к гр-ку ф-ии в этой точке параллельна оси ОХ. Если же ф-ия y=f(x) определена на отрезке [a,b], то в случае, когда она принимает наибольш. или наименш.знач. на одном из концов a или b и когда на этом конце существ. одностор.производная, то она не равна 0.

18.Производные второго и высших порядков.

Как указывалось ранее производная f’(x) ф-ии f(x) определённой на некотором интервале (a,b), представляют собой так же ф-ию, определённую на этом интервале. Может случится, что полученная ф-ия f’(x) сама является дифф-мой, т.е. имеет прроизводную.

Производная ф-ии y=f(x) от первой производной этой ф-ии называется её второй производной или производной второго порядка, которая обознач. f’’(x). Значит f’’(x)=( f’(x))’ по определению. Аналогичным образом определяется и производная ф-ии y=f(x) порядка большего чем 2. Так производные n-го порядка ф-ии y=f(x) по определению равна производной от производной n-1 порядка =( 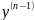)’. Таким образом из сказанного следует, что для вычисления производной n-го порядка ф-ии y=f(x) необходимо найти все производные порядка от 1-ой до n-1.

Формула Лейбница: формула Лейбница для вычисления такой производной напоминает ф-лу Бинома Ньютона, где вместо показателей показателей степеней записываются соответствующие производные: 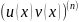= v+ v’+ +…+ .

20. Теорема Ролля

30 Направл. Выпукл. Графика ф-ции.

Будим говорть что график ф-ции y= f(x)имеет на интервале(а,б)выпукло сть направлен. Вниз(вверх)если график этой ф. в границах указанного интервала лежит не ниже(не выше)любой своей касательной.Т если ф.f(x)имеет на интервале (а,б) конечную производ.второго порядка и если эта произ. Не отриц.(не полож) в любой точке этого интервала то график ф-ции имеет на интервале(а,б) выпук-ость вниз(вверх)Алгоритм для определен выпукл.:1)найти перв. Произ.ф. y=f(x).2)найти втор. Произ. Ф(от перв. Производ)3)найти интервалы где f’’(x)>0, f’’(x)<0,4) получен.решение неравен-в указы вают на направл. Выпуклости ф-ции.

Пусть ф-ия y=f(x):

1.Определена и непрерывна на отрезке [a,b];2. Имеет в каждой точке интервала (a,b) производную;3. На концах этого отрезка ф-ия y=f(x) принимает равные значения, т.е. f(a)=f(b), тогда внутри отрезка найдётся такая точка с, что f(c)=0. Геометрически т.Ролля означает, что у графика, непрерывного на отрезке, и дифференцируемой внутри его ф-ии, которая принимает на концах отрезка равные значения, сущ-т точка, в которой касательная параллельна оси абсцыс.