
- •1.Функция, её обл.Опред.И мн-во знач. Спо-бы зажания ф-ии.
- •3.Числовыепоследти.
- •4.Предел числ.Послед.Опред, св-ва.Св-ва пределоа, св. С арифм.Оп.Над послед.
- •5.Монотонная послед.И еёпредел.Бесконечномал.И больш.Посл.
- •6.Предел фун-ии, св-ва пр-ов
- •8.Непрервывные в точке ф-ии, их св-ва.Точки разрыва ф-ии.
- •12.Физический и геометрический смысл производной.
- •10.Приращение арг-та и фу-ии.Опред-ие пр-ой. Одност. Пр. Условия сущ пр.
- •9.Первый замечательный предел(Дорисовать!)
- •13.Понятие дифференциала ф-ции.Применение дифф .В прибл. Вычислениях.
- •33 Асимптоты графика ф.
- •15. Обратная ф-ция и её дифф. Теорема о пр. Обратной ф-ции.
- •27Кри-рии монотон.Ф-ции
- •17. Теорема о дифференцируемости сложной ф-ии. Логарифмическая ф-ия.
- •19. Теорема Ферма
- •18.Производные второго и высших порядков.
- •20. Теорема Ролля
- •30 Направл. Выпукл. Графика ф-ции.
- •21. Теорема Лагранжа
- •32 Достаточ усл сущест. Перегиба
- •28 Локал. Экстем. Ф-ции.1ду (Дорисовать!)
- •31 Точки перениба графика ф-ции
- •22. Раскрытие неопр-ей.Правило Лопиталя
- •11.Дифференцируемость функции в точке.Критер.Диф.
- •26 Теорема о постоянстве ф-ции
- •24Формула Тейлора
- •29 Локал. Экстем. Ф-ции. 2 ду
(физический)Пусть
ф-ция S=f(t),
где t-время,
описывает з-н движения в мат. точке по
прямой линии. Придадим времени t
произвольное приращ. ∆t,
получим t+∆t,
кот. будет соответствовать
S+∆S=f(t+∆t).Откуда
следует, что пройденный путь получит
приращ. ∆S=
S+∆S-S.
Найдём разностное отн.
(г-ский)Рассм.
гр-к ф-ции y=f(x)
Пусть
дана М соотв. знач.
Кос-ной
к гр-ку ф-ции y=f(x)
в точке М будем наз. предельное положение
МР при стремлении в точке М к точке Р
по гр-ку или при усл. ∆х→0.Из рисунка
видно, что tg
12.Физический и геометрический смысл производной.
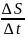 это отн. ук. на сред. скор. мат. точки на
пути ∆S.
∆t→0
и найдём предел разн. отн. и
это отн. ук. на сред. скор. мат. точки на
пути ∆S.
∆t→0
и найдём предел разн. отн. и
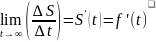 .Откуда следует, что пр. от пути по
времени равна мгновенной ск. движ. т.
в момент времени t.
Из сказанного следует, что если известна
ф-ла пути пройденной т-ой при неравн.
прямол. движ., то числено равна ск. движ.
точки в данный момент вр.Например,
чел-к движ. по з-ну:
S=
.Откуда следует, что пр. от пути по
времени равна мгновенной ск. движ. т.
в момент времени t.
Из сказанного следует, что если известна
ф-ла пути пройденной т-ой при неравн.
прямол. движ., то числено равна ск. движ.
точки в данный момент вр.Например,
чел-к движ. по з-ну:
S=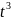 -3t+1.
Найти ск. движ. этого тела в момент вр.
t=2сек.
S’=3
-3t+1.
Найти ск. движ. этого тела в момент вр.
t=2сек.
S’=3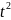 -3.
S(2)=3*
-3.
S(2)=3*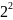 -3=9
-3=9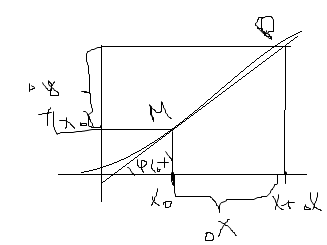
 ,
а точка Р соотв. знач. Ар-та
+∆х,
где ∆х явл. Некоторым приращ. ар-та.
Соед. точки М и Р прямой, кот назовём
секущей.ᵞ( ∆х)-угол, кот. Образует эта
секущ. с положит. нап. оси Ох, при этом
очевидно, что если менять расс. ∆х, то
будет меняться и угол. Будем неограниченно
прибл. точку Р к точке М по гр-ку ф-ции.
,
а точка Р соотв. знач. Ар-та
+∆х,
где ∆х явл. Некоторым приращ. ар-та.
Соед. точки М и Р прямой, кот назовём
секущей.ᵞ( ∆х)-угол, кот. Образует эта
секущ. с положит. нап. оси Ох, при этом
очевидно, что если менять расс. ∆х, то
будет меняться и угол. Будем неограниченно
прибл. точку Р к точке М по гр-ку ф-ции.
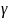 (∆х)=
(∆х)=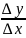 =
= .
Учитывая, что
.
Учитывая, что
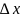 сремящаеся к 0 секущ. МР переходит в
кос., то
сремящаеся к 0 секущ. МР переходит в
кос., то
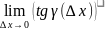 =
tg
=
tg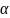 ,
где -угол, кот. обр. косательную с полож.
напр. оси Ох, с другой стороны
=
=
f’(x).
В рез-те получили, что f’(
)=
tg
,
а это значит, что пр-ная ф-ции f(x)
в точке
ровна угл. коэ. кас, графику ф-ции y=f(x)
в точке касания, а tg
называется угл. коэф. к гр-ку ф-ции в
данной точке
.
Отсюда легко написать ур-ния кас. гр-ку
ф-ции в данной точке. Исходя из ур-ния
прямой, проход. ч/з точку
и
,
где -угол, кот. обр. косательную с полож.
напр. оси Ох, с другой стороны
=
=
f’(x).
В рез-те получили, что f’(
)=
tg
,
а это значит, что пр-ная ф-ции f(x)
в точке
ровна угл. коэ. кас, графику ф-ции y=f(x)
в точке касания, а tg
называется угл. коэф. к гр-ку ф-ции в
данной точке
.
Отсюда легко написать ур-ния кас. гр-ку
ф-ции в данной точке. Исходя из ур-ния
прямой, проход. ч/з точку
и
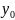 с угл. коэф. k.
y-
=k(x-
).Учитывая,
что k=
tg
=f’(
)
ур-ниe
касат. запишутся: y-
=f’(
)(x-
)
y=
+f’(
)(x-
с угл. коэф. k.
y-
=k(x-
).Учитывая,
что k=
tg
=f’(
)
ур-ниe
касат. запишутся: y-
=f’(
)(x-
)
y=
+f’(
)(x-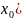 .
.
Пусть
дана ф-ия у= f(x),
опред.на некотором промеж.Х, конечн.или
бекскон.Зафиксируем любое знач.xо
из этого
промеж.И зададим арг-ту xо
нек-ое приращ.и обознач.через ∆x.
xо+
∆x.Тогда
знач.ф-ии у=f(x0)в
точке x0
тоже примет
знач.f(xо+
∆x).При
этом разность между знач.у= f(xо+
∆x)-
f(x0)
.Рассмотр.отн-е
Производной
ф-ии у=f(x)
в точке хо,
наз-ся предел отн-ия приращ.ф-ии к
приращ.арг-та, если такой предел сущ,
при условии что ∆x->0.Производная
ф-ии в точке x0
наз-ся числом, если рассм.произв.ф-ии
в каждой точке некоторого промеж.х, то
произв.уже становится ф-ей оХ Правосторонней
произв.ф-ии у=f(x)
в точке х0
наз-сяправост.предел
разностного отнош. при условии, что
Если
ф-ия у=f(x)
имеет в точке x0
пр.и лев. произв,скоторые совп., то и
ф-ия у=f(x)
имеет произв. в этой же точке
10.Приращение арг-та и фу-ии.Опред-ие пр-ой. Одност. Пр. Условия сущ пр.
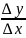 =
=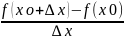 .Предел
lim
∆x->0
=lim
.Предел
lim
∆x->0
=lim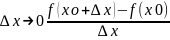
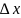 -> 0, если такой предел сущ.Пр.произв:
f’(x0+0),
лев - f’(x0-0).
-> 0, если такой предел сущ.Пр.произв:
f’(x0+0),
лев - f’(x0-0).
