6.Предел фун-ии, св-ва пр-ов
Пусть дана ф-ия y=f(x) и пусть дана точка а. Будем считать что точка а может не принадл.мн-ву Х, но в любой скольугодно малой окрестн.этой точки, обязат. принад.числа их мн-ва Х, не равные а.
Предел ф-ии(по Гейне): число b наз-ся пределом ф-ии f(x), при X->a, в точке а, если для люб.сходящюпослед. х1, х2,… хn значение арг-та Х, эл-ты которой отличны от а, соотв.послед-ть f(x1)…f(xn)…згачений ф-ии сходится к числу b.В этом случае говоряь, что ф-ия f(x) имеет предел в точке х=а.lim f(x)=b.Отсюда следует,что limf(xn)=b.
Рассмотрим ф-ию Дирихле:
f(х)= 1,если х=число рац. 0-если –число иррац.Эта ф-ия не имеет предела ни в одной точе а,беск.прямой х=а.Действ., если взять посл-ть рац.чисел, топосл.сх-ся к одному.если иррац. – к нулю., а это противоречитопределению предела ф-ии в точке а.
limCXn=C*limXn. Если послед . {Хn} сходи.и k-нат.число, то lim(xn)k=(lim xn)k.
Если lim{xn:Уn}= limXn: limYn, limXn =0 и limУn=0 либо limXn =∞ и limУn=∞ то поступают сл. образом:1) делим числ и зн.на наивысш.степень 2) умнож на сопр числ или знамен.
7.Одност-ие
пределы.Беск-мал и бес-бол.ф-ии, их ср-е Число
b
наз-ся правост.пределом ф-ии у=f(x),
при х->а, если для любой сходящейся к
числу а послед. х1
,х2,
...хn
..знач.арг-та
х, эл-ты которой больше числа а,
соотв.послед.f(
х1)
,f(х2)
...f(хn)
.. сходится
к числу b.
Прав. предел обознач.limf(x)x->a+0, Точка
х0
наз-ся предельной точкой числ.мн-ва Х,
если в люб.окр-ти этой точки содерж.
хотя бы одна точка и Х, отличн. от х0.
Ф-ия наз-ся
непрерывн.в точке х0,
если выполн.сл.требования:1)ф-ия определ.в
точке х0
т.е. х0
ϵD.
2) сущ.предел фэтой ф-тт при х-> х0
3) вып-ся
равенство
2.Точкой
разрыва ф-ии f(x)
может быть:а)точка в кот. эта ф-ия не
опред.б)точка в кот.сущ.одност.пределы,
знач.кот.не равно знач.ф-ии в этой
точкев) точка, в кот.сущ.различн.одност.предлы,
либо 1 из них не сущ. 1)устр.разрыв:точка
х=а наз-ся точк. устр.раз-ва ф-ии f(x),
если одност.пре-лы
сущ.и равны между собой в этой точке,
но в самой точке ф-ия либо не опред.либо
отличается от знач.одност.пре-лов.Пример:пусть
дана ф-ия f(x)= в
точе х=0 –устр разрыв, т.к. од.пределы
равны единицам, а f(0)=2<>1 Разрыв
перого рода:…ф-ии у=f(x),
если в этой точке ф-ия имеет конечные,
но не равные пр.и лев. пределы, т.е если
limf(x)x->a-0<>
imf(x)x->a+0.Нарим.:
ф-ия f(x)=sgn(x),
1- x>0,
0 – x=0,
-1- x<0.Лев
-1, пр 1, sgn(0)=0 Разрыв
второго рода:точка х=а наз-ся т.р.вт.рода
ф-ии у=f(x),
если в этой точке не имеет хотя бы 1-ого
из пределов, или хотя бы 1 из пр-ов равен
бесконечн.у=ctg(x),
т.к ctg(x)=
8.Непрервывные в точке ф-ии, их св-ва.Точки разрыва ф-ии.
=f(
х0),
а точка х0
наз-ся
точкой непрерывн.ф-ии f(x).
,
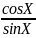sin(πn)=0,
cos(πn)=(-1,1).
Значит в этой точке предел бесконечен.