1.Функция, её обл.Опред.И мн-во знач. Спо-бы зажания ф-ии.
Функцией определённой на множестве Х называется правило, по которому каждому эл-у из мн-ва Х ставится в соответствие единств. эл-т y из мн-ва У.
х0ϵХ, у0ϵУ, f(X0)=y0, при этом у0 на-ся значением ф-ии f(x) в точке х0.
y=sinx, х0=π.
Ф-ия f(х) считается заданной, если указано првило, с помощью которого каждому эл-ту хϵХ поставлен в сооответствие уϵУ, при этом Х наз-ся обл-тью опред-ия данной функции, а мн-во У – обл-тью её знач.
Нахождение обл-ти опред-ия:
1)если ф-ия задана дробью со знамен-ем, то из обл-ти её определения исключены те зн-ия х, при которых зн-тель обращается в 0
2) если в формуле задающей ф-ию содер-ся корень чётной ст-ни, то то из обл.опр.исключаются те знач. переменной х, при которых выражение ,стоящее под знаком √ принимает отриц. значения.
3) если в ф-ле задающей ф-ию содержится log при любом допустимом осн-ии, то из обл.опр. искл-ся те те знач-ия переменной х, при которых выраж. под знаком log приобретает неположит. значения, причёём осн-ием лог-фа может быть только положит. число.
Способы задания:
1.аналитический(формула)
2.графичечкий(графиком)
Однозначная фунция – ф-ия, где каждому знач. x cоотв. единств. значение у
График одн. ф-ии – кривая, к-рая имеет не более одноф точки пересеч. с любой прямой, паралл. оси Оу.
Для того чтобы найти обл.опред – можно спроектировать точки графиков на ось иксов.
Обл знач. – на ось игриков.
2.Чётные и нечётные, монотонные и периодические фии.Определения и примеры.Ф-ия у=f(х), опр-ая на мн-ве Х наз-ся чётной, если её обл.опр.симм. отн-но начала коорд., т.е. если хϵХ -> -хϵХ и f(-х)= f(х). у=х4-2х2.Ф-ия у=f(х), опред-ая на мн-ве Х наз-ся неч, если её обл.опр.симм.отн-но нач.коорд. и для любого х имеет место равенство f(-x)=-f(x). у=х3+4х.График четн. ф-ии симм.отн-но оси ординат, а нечётн. – отн. нач. коорд.Сущ-ют ф-ии, которые и не чётн. и не нечётн. f(x)=x2+2x-3Ф-ия у=f(x), опред. на мн-ве Х, наз-ся периодической, если сущ.такое полож.чисто Т, что если х+TϵX, то х-TϵX и f(х+T)=f(x).График пер..ф-ии при смещ.его влево или вправо совпадает сам с собой.К элементарным ф-ям отн-ся линейная ,квадратичная, показ-я, логарифм., тригоном., а также функции, полученные из них с помощью арифм. действий.Неэлементраная у=sgnx, 1-если х>0, 0-если х=0, -1- х<0.Монотонные ф-ии:Ф-ия у=f(x), опред. на мн-ве Х наз-ся возрастающей на этом мн-ве, если для любых х1 х2 из мн-вы Х при условии х1 >х2 следует что f(х1)> f(х2). у=х2 (0;∞)Ф-ия у=f(x), опред. на мн-ве Х наз-ся убывающей на этом мн-ве, если для любых х1 х2 из мн-вы Х при условии х1 >х2 следует что f(х1)< f(х2).если >< заменить на ≤≥ то получим неубыв. или невозр. ф-ии на данном промеж-ке.монотонными наз-ся возр, убыв, невозр, неубыв. Функции
3.Числовыепоследти.
Операции над ними.Огр. и неогр. числовые послед-ти.
Если
кажд.нат.числу n
из мн-ва N
cтавить
в соотв. по опр. закону некоторое действ.
число х из мн-ва R,
то мн-во таких чисел Х наз-ся числ.послед.,
а сами числа- её эл-ми. Обозн-ся {xn}
.Числовая послед. имее бесеонечное
мн-во эл-ов. Т.к. мн-во нат.чисел бесконечно,
то {xn}=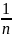
можно записать в развёрнутом виде
{xn}=
=
;
;
…Если
Хn
не
фиксируется, то n
общ.член послед-ти.Он указывает на то,
по какому правилу нах-ся члены
послед.Послед-ть считается заданной,
если отн-но люб.дейст.числа можно сказать
является ли оно чл. данной посл. или
нет.
Способы задания:
1)Перечислением нескольких нач.эл-ов, по которым можно определить правило образов.остальн.
2) Аналитический(формулой)
3)Рекурентный:дано неск-ко первых членов и формула x1=1 x2=2 xn=2xn-2+xn-1.
Операции:сложение, вычитание, умножение, деление.
Пусть {Хn}=x1 x2x3…xn {Yn}=y1 y2y3…yn. Суммой послед-тей {Хn} и {Yn} является послед. { Хn +Yn}, каждый член которой равен сумме соотв. членов данной послед-ти.Так же разность и произведение.В частном члены послед. {Yn} должны быть отличными от нуля.
Послед.наз-ся огранич.сверху, если сущ.такое действ.число МϵR, что для люб.члена послед. выполняется неравенство хn≤M, MϵR. M – верхняя граница послед., а хn≤M – условие огранич-ти послед.сверху.Любая огранич.сверху послед.имеет бесконеч.мн-во верхних граней(M1,M…).В кач. точной верхней грани принимается наименьшую грань M.Послед. наз-ся огранич., если она огранич. и св. и сн. Посл. {Хn} наз-ся неогран., если для любого действ. А, А>0, сущ. эл-т xnϵ{Хn}, такой что (хn)>A. {-n2} – огран. снизу.