13. Подвижные нагрузки в задачах статики. Расчётное положение нагрузки. Понятие о л.В.. Отличие от эпюр
Любая подвижная нагрузка вызывает появление сил инерции, но в приближённых расчётах её можно считать статической, вводя к найденным в процессе расчёта величинам динамическим коэффициентам.
Расчётное положение нагрузки можно найти 2 способами:
Рассмотреть множество вариантов расположения нагрузки на системе. Найти усилия и сравнить между любой.
При помощи линий влияния. В кач-ве базовой нагрузки рассмотреть единичную силу, направленную вертикально вниз.
Линия влияния какого-либо усилия- график, показывающий з-н изменения этого усилия в зав-ти от положения в сис-ме единичной силы, направленной вниз.
Построение л.в. можно произвести 2 способами:
Статический
Кинематический
Эпюра соответствует фиксированному положению нагрузки, она показывает усилия во всех сечениях конструкции.
Л.в. показывает усилия только в одном сечении от нагрузки, которая меняет своё положение.Каждая ордината л.в. –это значение данного усилия от единичной силы, располженная над данной ординатой.
14. Статический метод построения линий влияния. Л.В. Опорных реакций в балке
В основном применяются статический и кинематический методы построения л.в.
При использовании статического метода устанавливается аналитическая зависимость между искомым фактором и абсциссой z точки приложения единичной силы P=1. Затем в характерных сечениях вычисляются значения данного фактора и строится график (л.в.)
Составляются ур-я статики: сумма моментов относительно какой-либо точки, сумма проекций всех сил на вертикальную ось.
Рассмотрим балку на двух опорах с консолями, имеющую пролет l и длины консолей с1 и с2. положение подвижной силы P=1 будем определять координатой z, начало координат выберем на левой опоре. Приложения вертикальная нагрузка вызовет в опорах А и В вертикальные реакции Va и Vb.
∑Mb=0, Va*l-1(l-z)=0
∑Ma=0, -Vb*l+1z=0
Va=(l-z)/l
Vb=z/l
Полученные уравнения-это ур-я л.в. опорных реакций, они линейны и справедливы при соблюдении условия
–c1≤z≤l+c2
Прямые, изображающие л.в., могут быть проведены через любые две точки
Va(z=0)=1
Va(z=1)=0
Vb(z=0)=0
Vb(z=1)=1
15. Статический метод построения линий влияния. Линии влияния внутренних усилий в междуопорном сечении балки.
Удобно внутренние усилия выражать через опорные реакции не записуя аналитическ выраж, а используя построенные ранее линии влияния
Междуопорное сечение балки
Закономерности:
Для л.в Q лев и прав ветви параллельны.под сечением скачок на 1 вверх.
Для л.в М лев и прав ветви пересекаются под сечением.она образует излом,направленный вверх.
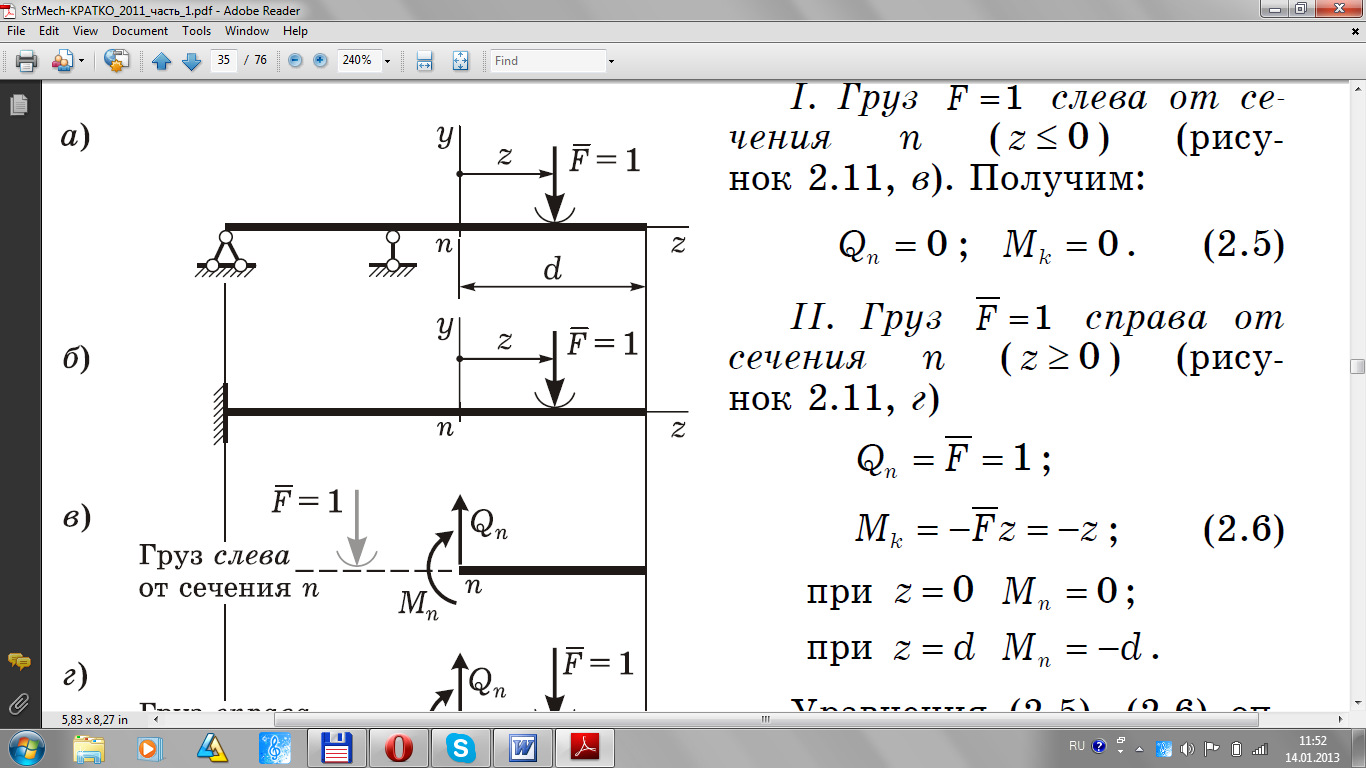
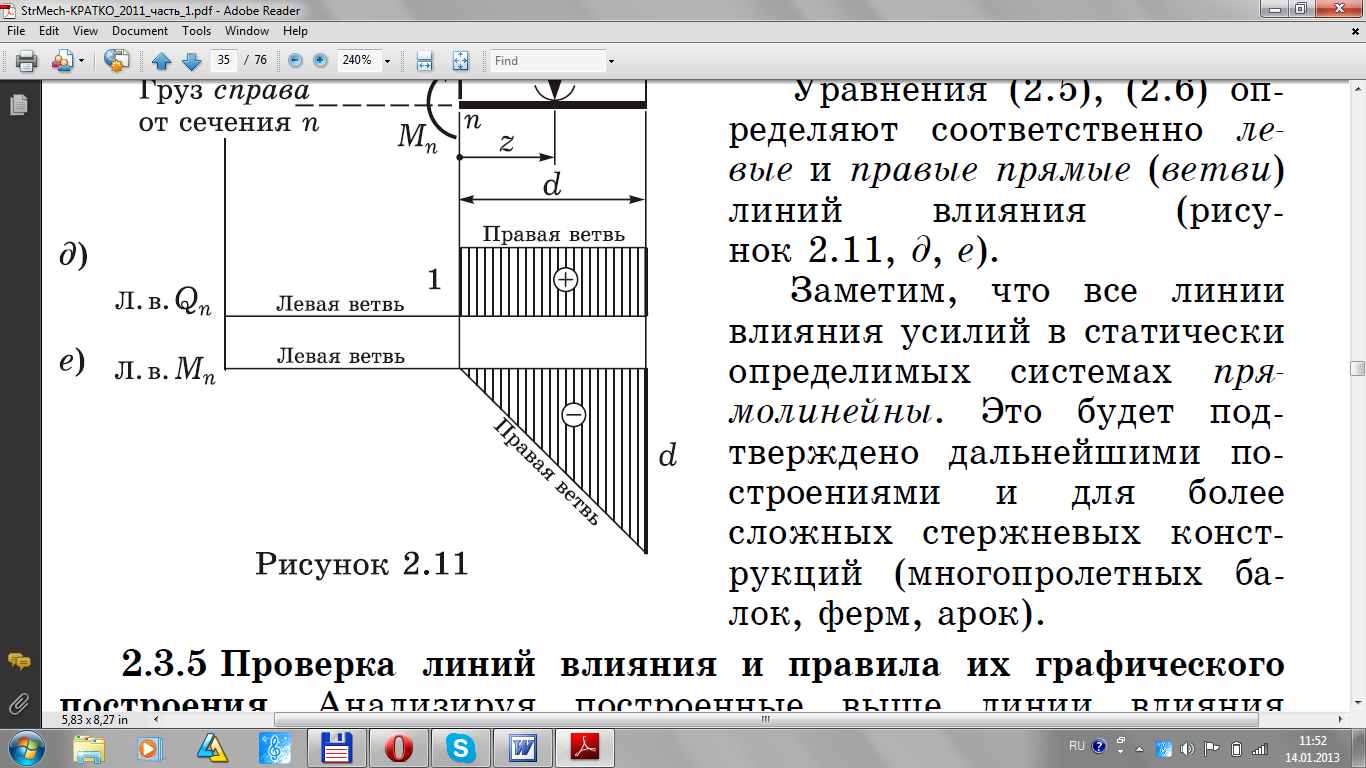
16. Статический метод построения линий влияния. Линии влияния усилий в консольном сечении балки.
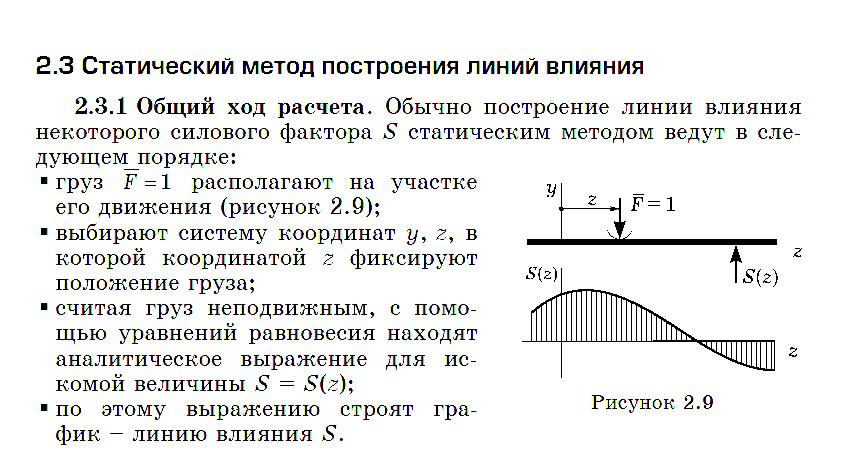
Статический метод построения линий влияния
Основан на составлении уравнений равновесия. Это возможно так как неподвижная нагрузка считается статической.
Порядок построения: 1.Сила F(с чертой)=1 располагается на участке его движения (рис.)
2. Выбирается система координат у,z, в которой координаты z фиксируют положения силы
3. Считая силу неподвижной с помощью уравнений равновесие определяем аналитическое выражение искомого силового фактора S=S(z)
4. По полученному выражению строим график л.в.
Линии влияния усилий в консольном сечении балки
