3 Связи и их характеристики

Каждая связь имеет две характеристики: статическая характеристика показывает, какие реакции возникают при удалении этой связи; а кинематическая характеристика показывает, каким перемещениям эта связь препятствует, а какие допускает.

1.2.1 Шарнирно-подвижная опора (стержень)

Поворот

Горизонтальное смещение

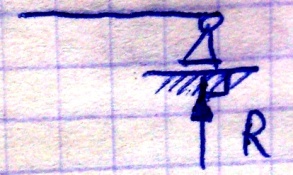
1.2.2 Шарнирно-неподвижная опора или шарнир

Поворот

Шарниры, соединяющие два элемента называются простыми, а более двух – сложными или кратными.

Простые

Сложные

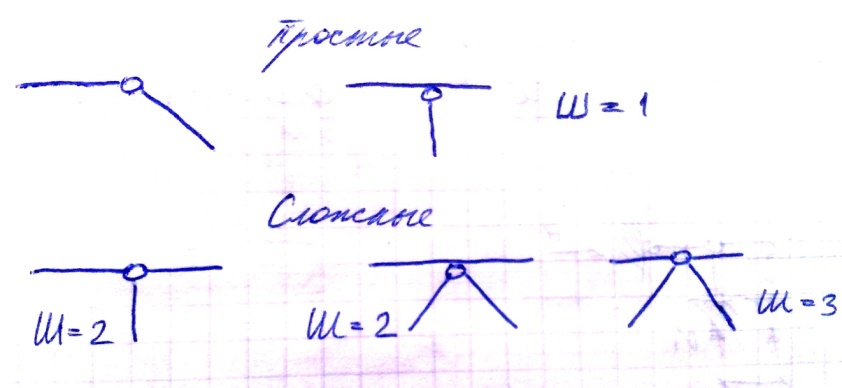
Кратность сложного шарнира определяется по формуле:

Ш=n-1, где n – число соединяемых элементов.

Кратный шарнир в расчетной схеме можно представить как несколько простых шарниров.

1

«заделка»

.2.3 Жесткое соединение

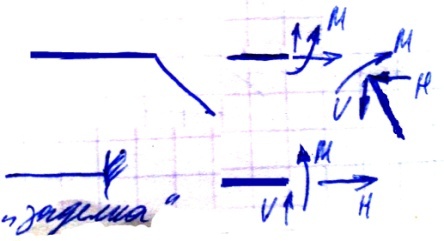
Жесткую заделку можно представить в виде 3-х не параллельных стержней.

Жесткое соединение можно представить в виде шарнира и стержня

Абсолютно жесткие

условные консоли

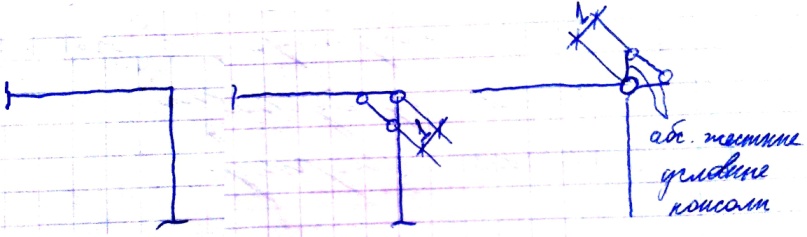
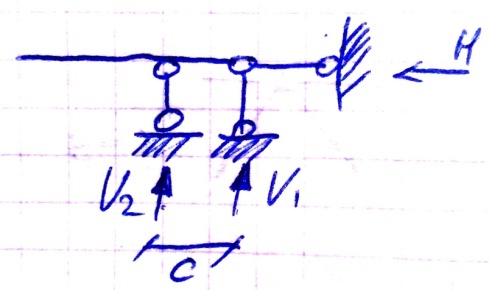
1.2.4 Скользящая заделка

Линейное перемещение

Эта заделка эквивалентна двум стержням

M = V_2*c

1.2.5 Упругоподатливое соединение

R = c·Δ

Произвольное перемещение

Малое перемещение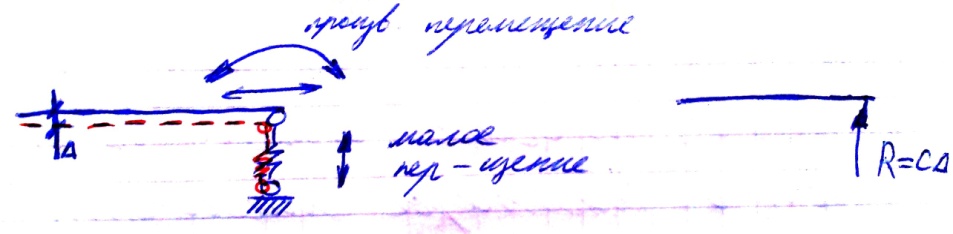

Δ- перемещение вдоль упругоподатливого стержня

с

Малый поворот

- жесткость стержня

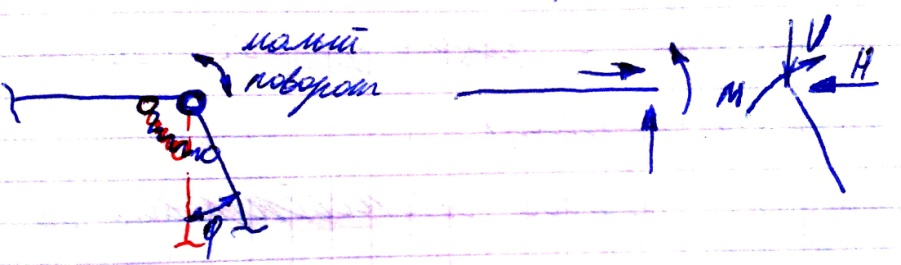
φ- взаимный угол поворота элемента

4. Основные уравнения строительной механики. Допущения строительной механики и следствия из них

Основные уравнения строительной механики.Исходные уравнения строительной механики можно разбить на три группы.

Уравнения равновесия (статики). Эти уравнения устанавливают взаимосвязь между внешними и внутренними усилиями, которые входят в них линейно. Таким образом, уравнения равновесия всегда линейные.

Уравнения совместности деформаций, представляющие геометрическую сторону задачи расчета сооружений. В этих уравнениях деформации связываются с напряжениями. В общем случае эти уравнения нелинейные. Но если учесть, что перемещения и деформации, как правило, малы, то уравнения, связывающие их, становятся линейными.

Физические уравнения связывают напряжения с деформациями или усилия с перемещениями. Они могут быть линейными и нелинейными, в зависимости от принятой физической модели.

Основные допущения строительной механики и следствия из них

Считаются допустимыми все гипотезы и допущения, что и в сопромате:

1) сплошности, однородности и изотропности;

2) идеальной упругости материала;

3)справедливости закона Гука (в основном курсе);

4) гипотеза плоских сечений Бернулли;

5) допущения о малости деформации.

Стержневые системы считаются достаточно жесткими, перемещение их точек малы по сравнению с размерами элемента. Допускается считать, что при изгибе точки смещаются перпендикулярно первоначальной оси, а уравнение равновесия допускается составлять по недеформированной расчетной схеме.

ω<<l

u<< ω

M=F_*l

M=F*l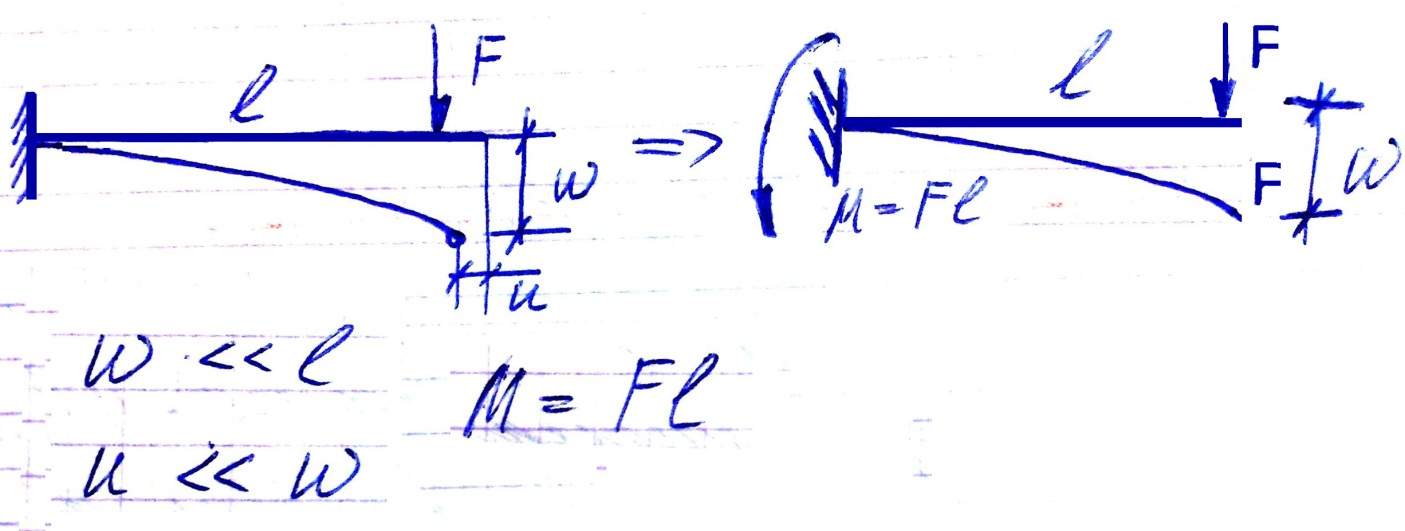

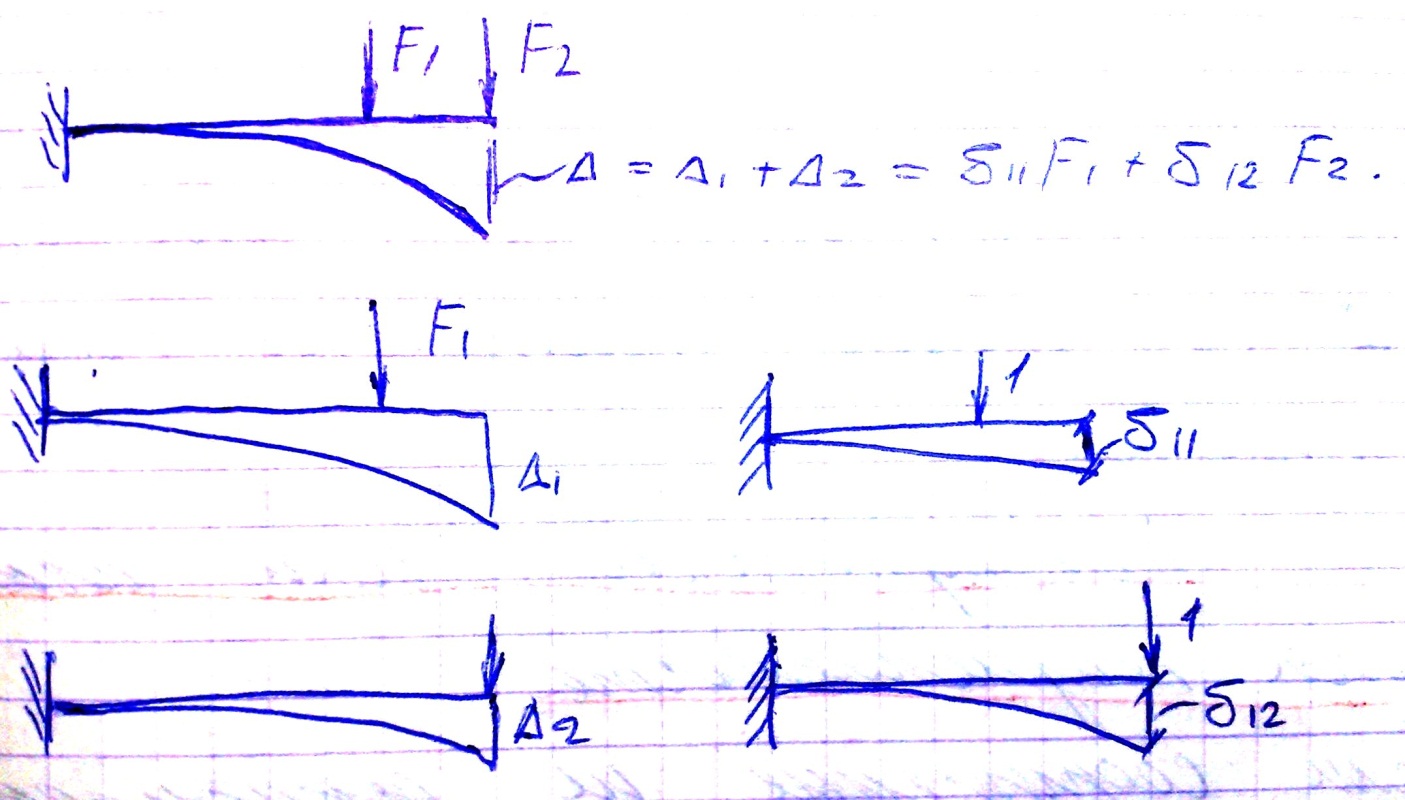
Принцип суперпозиции

Результат воздействия нескольких факторов равен сумме результатов каждого из них, приложенных по отдельности и независимо от порядка приложения. Также некоторую величину ( перемещение или реакцию) можно представить в виде произведения силы, ее вызывающей на аналогичную величину, вызванной единичной силой.