38.Расчётное положение подвижной нагрузки в арке
Прочность арок проверяется по нормальным напряжениям в крвйних точках попер.сечений, зависящих от изгибающих моментов и продольных сил. Будем рассматривать пологие строительные арки, напряжения в которых допускаетс определить без учёта кривизны.
Как загрузить арку врем.нагрузкой, чтобы получить наибольшее значение напряжения. В практ.расчётах арок исп-ют приём, основанный на разделении л.в. Ми N. Используют несколько положений:
- определ-сяопастное положение нагрузки по полож части л.в. М
-аналогично опр-сяопастное положение нагрузки от отр части л.в. М
-нах-ся опасное положение нагрузкипол.в. N, вычисляется значениепрод силы и соотв. Ему значение момента
-при каждом из указанных трёх положений опре-ся норм напряжения в крайних точках сечения и на них выбираются численно наибольшие для каждого знака.
Часто при приближённых расчётах арок расчётное положение нагрузки для каждого из характерных сеченийишут только по линии влияния изгибающих моментов.
39. Общая формула для определения перемещений от произвольных внешних воздействий
Рассмотрим систему, состоящую из прямолинейных стержней. Пусть система деформировалась в рез-те чего ее точки получили малое перемещение. Вырежем бескон малый эл-т сис-мы длиной ds, который испытывает деформации. Его первое сечение считается неподвижным.
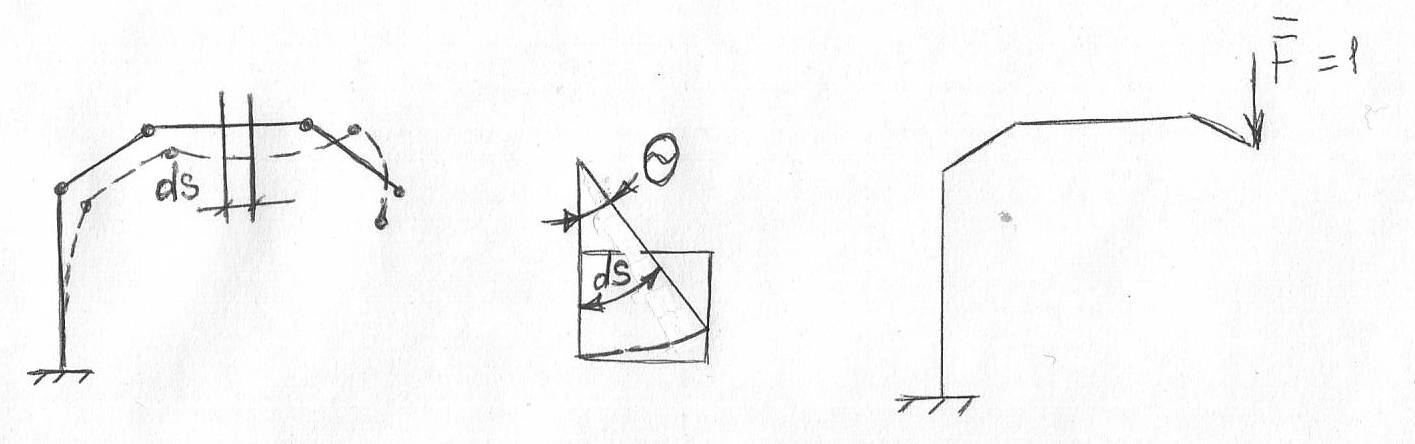
Рис 3
Вспомогательное состояние системы (рис3)
Допустим требуется найти вертикальное перемещение Δ точки К. для этого сформируем вспомогательное «единичное» состояние той же системы: по направлению искомого перемещения приложим единичную силу и определим возникшие от нее внутренние усилия. Будем считать что на эл-т ds не действуют сосредоточенные внешние силы, тогда приращениями dM, dQ, dN пренебрегаем.
Единичное состояние явл. состоянием равновесия, тогда согласно принципу Лагранжа сумма возможных работ сил этого состояния на любых возможных перемещениях =0.
Работа внешней силы
А(l)=P* Δ=1* Δ= Δ
dA(i)=(-N* Δs+Q* Δy+M*Θ)
A(i)=-∫ (-N* Δs+Q* Δy+M*Θ)
A(l) + A (i)=0
Δ=∫ (-N* Δs+Q* Δy+M*Θ)
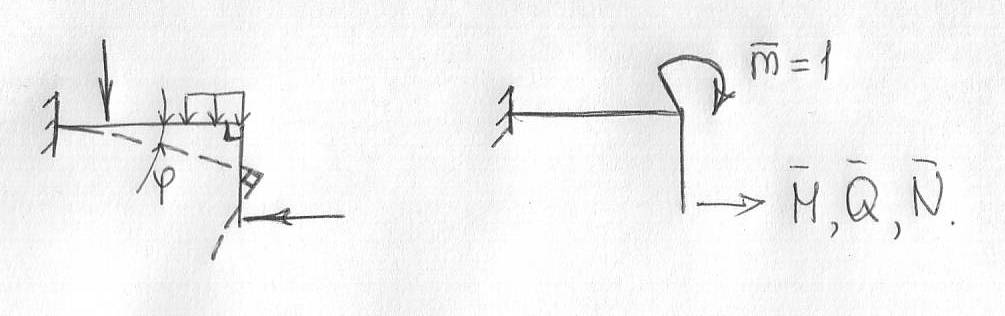
1. Чтобы выразить угловое перемещение , вместо единичной силы необходимо приложить единичный момент в заданном сечении , от которого найти внутренние усилия М,Q ,N.
2. полученную формулу можно использовать для статически определимых и неопределимых систем, также допускается ее использовать для стержней малой кривизны. Для стержней большой кривизны ее необходимо уточнить введением дополнительных слагаемых.
40. Формула Мора
Если на систему действует внешн. Нагрузка, то
Удлинение эл-та ds по аналогии с удлинением стержня длиной l опр-ся Δs=Np ds/EA (Δl= N l/EA)
Обозначим
- угол сдвига
Тогда
взаимный сдвиг сечений Δy=
ds
Угол сдвига определим из закона Гука
=G
касательное напряжение.Опр-ся по формуле
(при чистом сдвиге)
Это в том случае,если они распеределены равномерно,однако мы рассмотрим общий случай
Поэтому
введем поправку в формулу:
Qp/A
η -коэф.,учитывающий неравномерность распределения касат. Напряжений по сечению.
Δy=
ds=
ds/G=ηQpds/GA
η зависит только от формы сечения
-радиус
кривизны изогнутой оси
По известной
зав-ти сопр.материалов опр-ся по формуле
1/
=Mp/EI
После поворота сечений,ось эл-та ds изгибается по дуге окружности
Тогда
ds=
,
следовательно 
=ds/
=Mpds/EI
Δ=
Формула Мора
EA, GA, EI –жесткость попер. сечений при раст. сжат. сдвиге. изгибе
Np, Qp, Mp – внутр усилия, вызванные заданной внешне нагрузкой
N, Q, M – внутр усилия от единичной силы, приложенные в направлении искомого перемещения.
Порядок вычисления перемещения по формуле Мора:
Найти внутр усилия в сис-ме от нагрузки Np, Qp, Mp
По направлению искомого перемещения приложить ед усилия(для линейных перемещений-силу,для угловых-момент) и найти внутр усилия N, Q, M
Выч-ть интегралы Мора. Для сложной системы интегралы вычисляются на отдельных участках и результаты складываются.