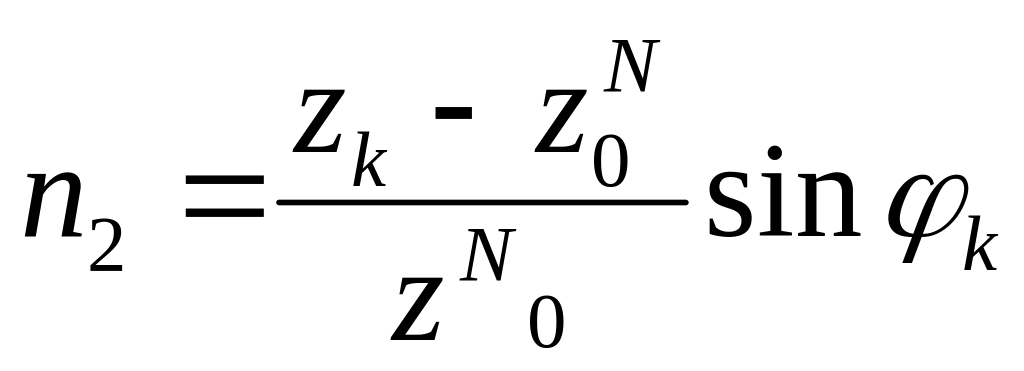- •Предмет и задачи строительной механики
- •2 Сооружение и его расчетная схема
- •3 Связи и их характеристики
- •Основные уравнения строительной механики. Допущения строительной механики и следствия из них
- •5. Геометрически изменяемые и неизменяемые системы. Диск. Связи абсолютно необходимые и лишние (избыточные).
- •6. Мгновенно изменяемые системы. Центр вращения. Фиктивный шарнир.
- •Число степеней свободы и степень изменяемости плоской стержневой системы
- •Кинематический анализ сооружений: аналитические методы. Необходимое аналитическое условие геометрической неизменяемости.
- •10.Основные свойства статически определимых систем
- •11. Методы расчета на статическую нагрузку статически определимых систем.
- •12. Кинематический метод опред усилий от неподвижной нагрузки. Применение принципа возможных перемещений для нахождения усилий в статически определимых системах.
- •13. Подвижные нагрузки в задачах статики. Расчётное положение нагрузки. Понятие о л.В.. Отличие от эпюр
- •14. Статический метод построения линий влияния. Л.В. Опорных реакций в балке
- •15. Статический метод построения линий влияния. Линии влияния внутренних усилий в междуопорном сечении балки.
- •16. Статический метод построения линий влияния. Линии влияния усилий в консольном сечении балки.
- •17.Проверка линий влияния в балках и правила их графического построения.
- •18. Кинематический метода построения линий влияния. Модели линий влияния раз - личных усилиях.
- •19.Определение усилий от неподвижной нагрузки по линиям влияния (вертикальных сосредоточенных сил, распределенной нагрузки, сосредоточенных моментов)
- •20 Коляда
- •21. Невыгоднейшее(расчётное, опасное) загружение линий влияния.
- •22. Расчёт многопролётных балок и рам на неподвижную нагрузку. Поэтажные схемы.
- •23. Линии влияния в многопролетных балках (статический и кинематический методы).
- •24.Фермы и их расчетные схемы. Основные элементы ферм. Статическая определимость плоских ферм
- •25.Фермы. Общая характеристика и классификация ферм
- •27. Линии влияния продольных сил в фермах: статический метод
- •29. Назначение и типы шпренгелей. Расчетная схема шпренгельной фермы. Определение усилий от неподвижной нагрузки.
- •31.Основные параметры трехшарнирной системы. Типы трехшарнирных систем. Определение опорных реакций.
- •33.Уравнение рациональной оси трехшарнирной системы. Действие равномерно распределенной нагрузки, сосредоточенных сил и радиальной нагрузки.
- •34. Линии влияния опорных реакций в трехшарнирной системе.
- •35.Линия влияния изгибающего момента в трехшарнирной системе: способы наложения и нулевой точки
- •36. Линии влияния поперечных сил в трехшарнирной арке.
- •37. Линии влияния продольных сил в трехшарнирной арке.
- •38.Расчётное положение подвижной нагрузки в арке
- •39. Общая формула для определения перемещений от произвольных внешних воздействий
- •40. Формула Мора
- •41.Частные случаи применения формулы Мора
- •43. Статически неопределимые системы и их свойства. Типы связей. Степень статической неопределимости.Особенности расчёта стат. Опр. Систем.
- •44.Основная система и основные неизвестные метода сил
- •46. Канонические уравнения:
- •47. Определение внутренних усилий в заданной статически неопределимой системе
33.Уравнение рациональной оси трехшарнирной системы. Действие равномерно распределенной нагрузки, сосредоточенных сил и радиальной нагрузки.

34. Линии влияния опорных реакций в трехшарнирной системе.
Вертикальные состовляющие реакций Va и Vb опред. из уравнений моментов отн-но центров опор.
∑MB=0; - VAL + P(L – z) = 0; VA = (L – z) / L
∑MA=0; VBL – Pz = 0; VB = z / L
При распол. сила Р=1 над опорой А ( z=0) Va=1, Vb=0. Над опорой В (z=1) Va=0, Vb=1.
Распор Н определяем рассматривая два варианта положения груза Р=1. Составляем уравнения моментов относительно шарнира С той части арки (левой или правой), на которой в данный момент нет подвижного груза.
∑MCправ=0;
VBL2-Hf=0;
H=![]() (уравнение левой прямой)
(уравнение левой прямой)
∑MCлев=0;
-VАL1+Hf=0;
H=![]() (уравнение правой прямой)
(уравнение правой прямой)
Слава от шарнира С изобразаем левую прямую (z<L1), справа – правую (z>L1). Их пересечение дает искомую л. вл. Н.
35.Линия влияния изгибающего момента в трехшарнирной системе: способы наложения и нулевой точки
Пусть сечение К имеет координаты zK, yK и угол наклона φK. Л.вл. изгиб. момента МК строится на основании выражения:
л.вл. МК = л.вл. МКБАЛ – уК(л.вл. Н)
Это значит, что л.вл. МК можно получить, построив л.вл. МКБАЛ, умножив их на соответствующие коэффициенты, а затем сложив ординаты. Прямые, ограничивающие линии влияния, носят названия: левая прямая – от опоры А до сечения К; средняя прямая – от сечения К до шарнира С; правая прямая – от шарнира С до опоры В.
Метод нулевых точек
1) необх. найти Z0M и отметить нулевую точку на линии влияния;
2) под шарниром А отложить ординату zK, через полученную точку и нулевую точку провести среднюю прямую (справедливую между сечением К и шарниром С);
3) ординату средней прямой под под сечением К соединить с нулем под опорой А – получится левая прямая;
4) ординату средней прямой под шарниром С соединить с нулём под опорой В – получится правая прямая.
36. Линии влияния поперечных сил в трехшарнирной арке.
Способ
наложения: пусть сечение К имеет
координаты
![]() ,
,
![]() и
угол наклона
и
угол наклона
![]() .
Л.в.
поперечной силы в этом сечении строится
на основании ее общего выражения
.
Л.в.
поперечной силы в этом сечении строится
на основании ее общего выражения
![]()
Значит,
л.в.
![]() можно
получить, построив л.в. Н и
можно
получить, построив л.в. Н и
![]() и
затем умножив их на соответствующие
коэффициенты и сложив ординаты.
и
затем умножив их на соответствующие
коэффициенты и сложив ординаты.
Порядок
построения л.в.
![]() методом
нулевых точек:
методом
нулевых точек:
найти
 и
отметить нулевую точку на линии влияния,
и
отметить нулевую точку на линии влияния,под шарниром А отложить ординату
 ,
через
полученную точку и нулевую точку
провести среднюю
прямую
(справедливую между сечением К и шарниром
С),
,
через
полученную точку и нулевую точку
провести среднюю
прямую
(справедливую между сечением К и шарниром
С),параллельно средней прямой через шарнир А провести левую прямую ( справедливую между опорой А и сечением К),
ординату средней прямой под шарниром С соединить с нулем под опорой В – правая прямая.


![]()
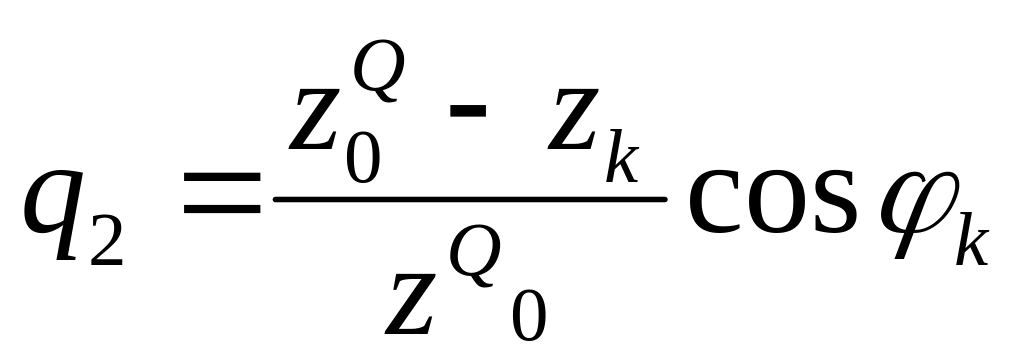

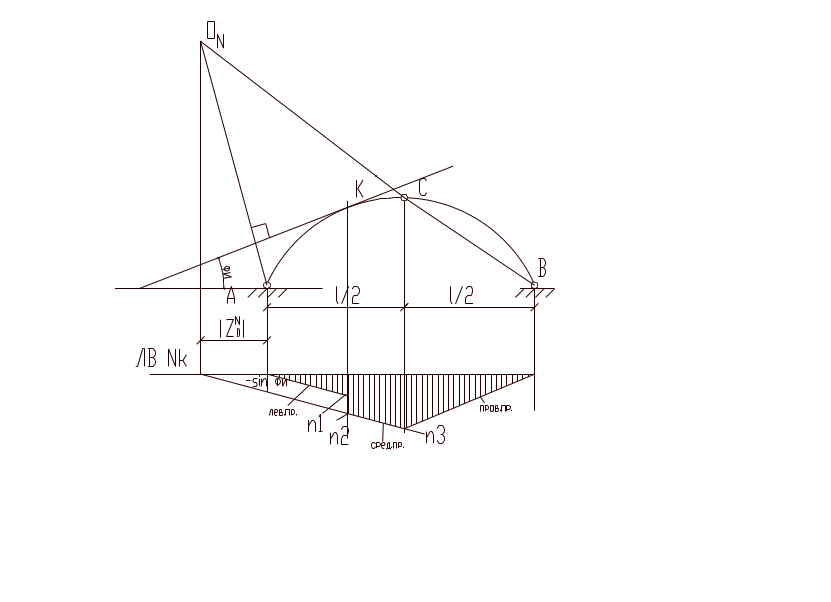
37. Линии влияния продольных сил в трехшарнирной арке.
Способ наложения: пусть сечение К имеет координаты , и угол наклона . Л.в. продольной силы в этом сечении строится на основании ее общего выражения
![]()
Значит,
л.в.
![]() можно
получить, построив л.в. Н и
можно
получить, построив л.в. Н и
![]() и
затем умножив их на соответствующие
коэффициенты и сложив ординаты.
и
затем умножив их на соответствующие
коэффициенты и сложив ординаты.
Порядок
построения л.в.
![]() методом
нулевых точек:
методом
нулевых точек:
найти
 и отметить нулевую точку на л.в.,
и отметить нулевую точку на л.в.,под шарниром А отложить ординату (
 ),
через полученную точку и нулевую точку
провести среднюю прямую(справедливую
между сечением К и шарниром С),
),
через полученную точку и нулевую точку
провести среднюю прямую(справедливую
между сечением К и шарниром С),параллельно средней прямой через шарнир А провести левую прямую ( справедливую между опорой А и сечением К),
ординату средней прямой под шарниром С соединить с нулем под опорой В – правая прямая.

![]()