31.Основные параметры трехшарнирной системы. Типы трехшарнирных систем. Определение опорных реакций.

Трехшарнирные системы относятся к распорным систе­мам, которые характеризуются тем, что вертикальные нагрузки вызывают горизонтальные опорные реакции — распор H (рис. 1, а,б,в).Это могут быть конструкции различного типа – рамы, арки, фермы, которые состоят из двух дисков, соединённых между собой шарниром и шарнирно присоединенные к земле.

Т рехшарнирной аркой называется трехшарнирная система из двух криволинейных брусьев (рис. 1, а).

H

H

H

H

H

H

a

b

в

Рис. 1

y

a

b

a₁

F

q

Ключевой шарнир арки C – шарнир, соединяющий левый и правый диски арки. Как правило, он лежит на оси симметрии.

Стрела подъема арки f – расстояние от наиболее удаленной точки оси арки (ключа) до линии, соединяющей центры опор.

Пролет арки l – расстояние между опорными вертикалями.

А,В- пяты.

С

f

x

В

А

H

H

l/2

l/2

V_A

V_B

l

q

F

B

А

С

V_A^Б

V_B^Б

Рис.2

Определение опорных реакций

Рассмотрим эту задачу на примере арки, изображённой на рис.2. При этом будем делать сравнительный анализ реакций и усилий в арке и в балке одинакового пролёта и одного и того же загружения. Выразим длину распределения нагрузки q через l и а. Тогда а₁=l/2-a.

Вертикальную реакцию V_A определим из уравнения статики

отсюда

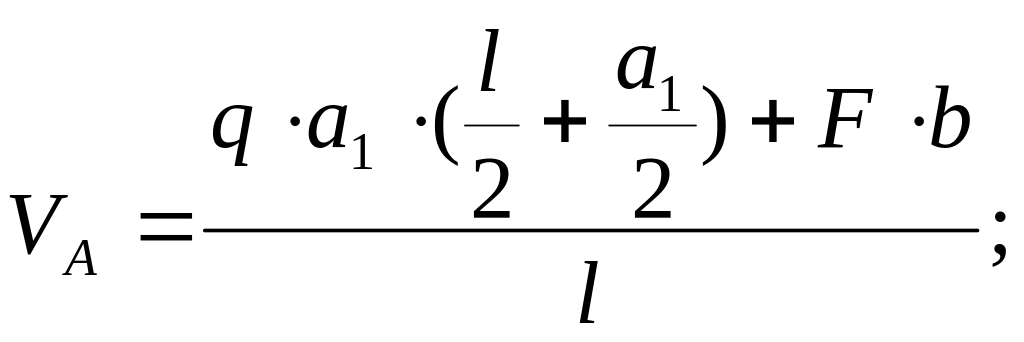
Вертикальную реакцию V_B определим из уравнения статики

отсюда

Если подставить выражения V_А и V_В проверка выполняется. Так как все реакции положительны, их направление изначально выбрано верно.

При определении вертикальных реакций в балке используются те же уравнения статики. Поэтому вертикальные реакции в арке и балке одинаковы.

Определим горизонтальные реакции. Если имеют место только вертикальная нагрузка, эти реакции будут равны, поэтому обозначать их будем H, полагая, что из уравнения статики .

Рассматривая равновесие арки целиком, мы не сможем подобрать уравнение статики для определения распора H. Поэтому сделаем сечение через шарнир С и рассмотрим равновесие, например, левой части арки (рис. 3). Сечение прове-

H

f

А

a

V_A

a₁

q

дено через шарнир, а значит в нём отсутствует изгибающий момент и возникают только поперечная сила Q_С и продольная сила N_С. Так как нас интересует значение реакции Н, будем использовать уравнение статики

N_C

С

Q_C

l/2

V_A^Б

А

С

q

l/2

Q_C^Б

Рис.3

Для проверки правильности вычисления распора можно определить его ещё раз из равновесия правой части, используя уравнение

Обратим внимание, что числитель в выражении распора есть балочные момент в сечении С. Тогда выражение для определения распора можно представить следующим образом . Из этого выражения видно, что чем меньше стрела подъёма f, тем больше значение распора при одной и той же нагрузке. Таким образом, отличительной особенностью работы арки (и распорных систем в целом) является то, что в них может возникать распор большой величине (превышающий значения внешних нагрузок). Значение его тем больше, чем меньше стрела подъёма арки. Это требует установки специальных опорных устройств, препятствующих «расползанию» арки по горизонтали. В случае, если арка опирается на основание, которое не обладает соответствующим требованиям, то горизонтальный распор можно передавать на затяжку. Такая арка имеет три опорных связи (горизонтальная реакция опоры А равна нулю) . Так как одна внешняя связь удаляется, устанавливается одна дополнительно внутренняя связь – затяжка, работающая на растяжение.

Затяжка может устанавливаться на уровне опор, либо быть повышенной. Возможен случай комбинированной затяжки (рис. 4.4).

32.

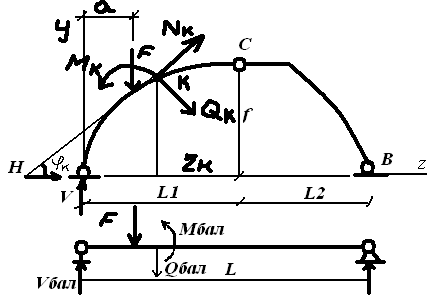
Каждое сечение хар-ся 3мя геом. параметрами: лин. параметры z_K, y_Kи уклон φ_K.

Внутр. усилия арки удобно выражать через усилия в соотв. балке. Составим уравнение равновесия левой части конструкции:

∑М_К=0. арка: М_К + Ну_К + F(z_K – a) – V_Az_K = 0; F(z_K – a) – V_Az_K = -M_K^БАЛ.

балка: M_K^БАЛ + F(z_K – a) - V_Az_K = 0.

M_K^БАЛ= -F(z_K – a)+ V_A^БАЛz_K. M_K = M_K^БАЛ - Ну_К

∑h = 0; - Q_K - Hsinφ_K - Fcosφ_K + V_Acosφ_K = 0.

Q_K = (- F + V_A)cosφ_K - Hsinφ_K

балка: ∑Y = 0. Q_K^БАЛ = - F + V_A^БАЛ. Q_K = Q_K^БАЛcosφ_K - Hsinφ_K

арка: ∑t = 0; N_K - Fsinφ_K + V_Asinφ_K + Hcosφ_K = 0.

N_K = (F – V_A)sinφ_K - Hcosφ_K. N_K = - Q_K^БАЛsinφ_K -Hcosφ_K

Выводы

1) при одинак. нагрузке изгиб.моменты и поп. силы в 3шарнирной системе всегда меньше, чем в соотв. балке (М<M^БАЛ)

2) прод. силы N всегда меньше 0, т.к. в последней формуле 2е слагаемое по модулю больше, т.е. | Hcosφ_K|>| Q_K^БАЛsinφ_K|. Hcosφ_K>0.

т.е. арка работает на внецентренное сжатие.

3) эпюры M,Q,N в арке всегда криволин., т.к. полученные формулы содерж. функции sinφ_K , cosφ_K , которые вдоль пролета меняются нелинейно.