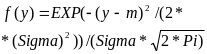5.1. Цель работы.

5.2. Исходные данные.

5.3. График зависимости ускорения от скорости автомобиля.

5.4. Схема обгона и расчетные формулы.

5.5. Схема алгоритма расчета.

5.6. Распечатка программы для ЭВМ.

5.7. Распечатка результатов расчета.

5.8. Графики зависимости "путь─время".

5.9. Выводы.

Лабораторная работа № 4

ГЕНЕРАЦИЯ СЛУЧАЙНЫХ ЧИСЕЛ ПО РАЗЛИЧНЫМ

ЗАКОНАМ РАСПРЕДЕЛЕНИЯ

1. Цель работы

Изучить методы разработки алгоритмов и программ генерации псевдослучайных чисел на ЭВМ.

2. Исходные данные

Закон распределения случайной величины Y, параметры распре­деления и алгоритм получения псевдослучайных чисел X, равномерно распределенных в интервале [0, 1], принимается по табл.1 в соответствии с номером варианта. Схемы алгоритмов получения рав­номерно распределенных случайных чисел приведены на рис. 1 - 3.

Таблица 1

Варианты исходных данных

N вари- анта	N алгоритма получения X	закон распределения Y и плотность вероятности f(y)	параметры распределения
1 5 9 13	1 2 3 2	Нормальный	m = 2 ; 3 Sigma = 0,5 ; 0,8
2 6 10 14	1 2 3 1	Экспоненциальный	Lambda = 1/m m=3 ; 4
3 7 11	1 2 3	Релея	D = 2*m /Pi m = 4 ; 5
4 8 12	1 2 3	Эрланга	Lambda = k/m m = 2 ; 3 k = 5 ; 6

P i =3.141592653

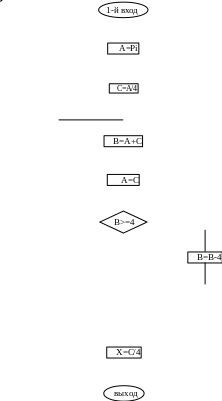
Схема алгоритма № 1 получения псевдослучайных чисел X

С=В

Рис. 1

Схема алгоритма № 2 получения псевдослучайных чисел Х

Х=0

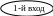
Рис. 5.2

А=0.011

А=А+1Е-8

x=frac(x/A+Pi)

[

frac операция выделения

дробной части результата

Схема алгоритма № 3 получения псевдослучайных чисел Х

х=1Е-6

x=frac(11х+Pi)

frac_операция_выделения

дробной_части_ результата

[

Рис. 3

3. Содержание работы

3.1. Разработать алгоритм и программу получения псевдослу­чайных чисел, распределенных по заданному закону.

3.2. В соответствии с исходными данными получить 40 псевдослучайных чисел.

3.3. Полученные случайные значения представить в виде ин­тервального статистического ряда. Построить гистограмму частостей случайных значений и теоретическую кривую плотности вероятности. Число интервалов статистического ряда принять равным 6.

4. Теоретические основы работы

Для того, чтобы от случайных чисел X, распределенных равно­мерно в интервале [0, 1], перейти к случайным числам Y, распреде­ленным по заданному закону, используются следующие формулы:

1) нормальное распределение

где r>=6;

рекомендуется принимать r=10 …15;

Таким образом, для получения одного случайного значения у следует просуммировать r случайных значений х;

2) экспоненциальное распределение

у = - m*ln(x) ;

3) распределение Релея

4) распределение Эрланга

т.е. для получения одного случайного значения у необходимо просуммировать k случайных значений х.

5. Содержание отчета

5.1. Цель работы

5.2. Исходные данные

5.3. Алгоритм расчета

5.4. Распечатка программы и результатов расчета

5.5. Статистический ряд, гистограмма частостей и функция плотности вероятности

5.6. Выводы

Лабораторная работа № 5

ПРИМЕНЕНИЕ ЭВМ ДЛЯ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ ДАННЫХ

1. Цель работы

Получение практических навыков составления программ для статистической обработки данных.

2. Исходные данные

Закон распределения случайной величины Y и параметры распределения принимаются по табл. 1 из лаб. работы № 4 в соответствии с номером варианта. Для получения псевдослучайных чисел X, равномерно распределенных в интервале [0, 1], использовать алгоритмы, схемы которых приведены на рис. 1 - 3 в лаб. работе № 4; варианты 1, 2, 3, 4, 14 - рис. 2; варианты 5, 6, 7, 8, 13 - рис. 3: варианты 9, 10, 11, 12 - рис. 1.

3. Содержание работы

3.1. Разработать алгоритм и программу, которые обеспечивают

- генерацию значений случайной величины Y;

- расчет оценок математического ожидания и среднего квадратического отклонения случайной величины на основании полученной вы­борки;

- получение интервального статистического ряда частот.

3.2. В соответствии с исходными данными получить и вывести на печать массивы из 50 и 200 псевдослучайных чисел, оценки математичес­кого ожидания и среднего квадратического отклонения, границы ин­тервалов и интервальный статистический ряд частот.

4. Теоретические основы работы

Оценка математического ожидания случайной величины, предста­вляющая собой среднее арифметическое, рассчитывается по формуле

где

- случайные значения ; N - объем выборки.

Суммирование случайных значений целесообразно выполнять в процессе их генерации.

Р асчет оценки среднего квадратического отклонения проводится по формуле

Случайные значения выбираются из массива, куда они предварительно записываются в процессе генерации.

Для получения интервального статистического ряда необходимо определить число интервалов К из выражения

К = trunc(1 + 3,2*lg(N)) + 1 ,

где trunc - означает операцию выделения целой части результата. Затем следует найти длину интервала

h = (y_max - y_min)/K ,

где - y_max и y_min - максимальное и минимальное значения вы­борки, которые целесообразно определить на этапе генерации слу­чайных

чисел y_i.

Далее вычисляются номера интервалов j, в которые попадают значения y_i.

j = trunc((y_i - y_min )/h) + 1 , i = 1,2,...N

Поскольку при использовании указанной формулы значению уmах соответствует интервал с номером К+1, необходимо проверять условие j<=K и при его невыполнении сделать присвоение j=K.

После нахождения номера интервала, в который попадает оче­редное значение y_i, соответствующий счетчик числа попаданий в этот интервал увеличивается на единицу:

m_j = m_j + 1

В результате, после просмотра всех значений y_i, получаем массив частот m_j, j = 1, 2,...,К, который показывает распределе­ние значений случайной величины по интервалам.

5. Содержание отчета

5.1. Цель работы

5.2. Исходные данные

5.3. Алгоритм расчета

5.4. Распечатка программы и результатов расчета

5.5. Выводы

Лабораторная работа № 6

ИССЛЕДОВАНИЕ РАСПРЕДЕЛЕНИЙ СЛУЧАЙНЫХ ВЕЛИЧИН

1. Цель работы

Изучить методику проверки согласия эмпирического и теорети­ческого распределений случайной величины.

2. Исходные данные

Выборка случайной величины (40 значений), полученная в ре­зультате выполнения лабораторной работы № 4.

Исходные данные записать в файл RNDID..DAT.

3. Содержание работы

3.1. По программе RND.EXE произвести расчеты по определе­нию статистических характеристик случайной величины и аппроксима­ции ее эмпирического распределения теоретическим законом наиболее подходящим по критерию Романовского. Результаты расчета содержатся в файле RNDNR.

3.2. Повторить аппроксимацию эмпирического распределения теоретическим законом, указанным в задании лабораторной работы № 4.

3.3. Проверить гипотезу о согласовании эмпирического и за­данного теоретического распределений по критерию хи - квадрат при уровне значимости alfa = 0,2 и 0,05 и по критерию Мизеса-Смирнова (омега-квадрат) при alfa = 0,2 и 0,1.

3.4. Построить графики эмпирической и теоретической функций распределения и проверить гипотезу о согласовании эмпирического и заданного теоретического распределений по критерию Колмогорова при уровне значимости alfa = 0,1.

4. Теоретические основы работы

Структурная схема алгоритма программы RND для исследования распределений случайных величин приведена на рис. 1

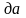
После обращения к программе задают вид распределения случай­ной величины (в данном случае непрерывное) и в качестве наимено­вания данных вводят номер учебной группы, номер варианта и вид закона распределения (указанный текст набирается через пробелы без запятых). Затем задают объем выборки и поочередно вводят слу­чайные числа. По завершении ввода, при необходимости, в исходные данные вносятся исправления, для чего следует положительно отве­тить на соответствующий вопрос программы и набрать порядковый номер числа, которое необходимо исправить.

Число интервалов следует задавать равным значению, рекомен­дуемому программой, а величину смещения принимать равной 0.

Затем необходимо выбрать наилучшее теоретическое распределе­ние по критерию Романовского. Это достигается в результате поло­жительного ответа на соответствующий вопрос программы.

На следующем этапе рекомендуется получить графики теорети­ческого и эмпирического распределений, а также помимо значений критериев хи-квадрат и Романовского - значение критерия Мизеса.

В дальнейшем следует продолжить расчет (положительно ответить на соответствующий вопрос) и, не изменяя числа интервалов и величины смещения, ввести порядковый номер тре­буемого закона распределения из списка, предложенного программой. После получения значений параметров распределения, теоретических частостей и значений критериев расчет можно закончить.

Для проверки гипотезы о согласовании теоретического и эмпи­рического распределений по критерию хи-квадрат необходимо по таб­лице найти граничные значения хи-квадрат при заданных уровнях значимости и известном числе степеней свободы (взять из распечат­ки результатов расчета). Затем следует сравнить значение хи-квадрат, полученное в результате расчета, с табличными значениями и сделать соответствующие выводы о подтверждаемости гипотезы при различных уровнях значимости.

С целью проверки гипотезы по критерию Мизеса-Смирнова следу­ет по таблице найти значение функции распределения статистики омега-квадрат в точке, полученной в результате расчета (значение критерия Мизеса в распечатке). Найденное значение необходимо срав­нить с доверительными вероятностями, которые определяются по за­данным уровням значимости, и сделать соответствующие выводы о подтверждаемости гипотезы.

Для построения графиков эмпирической и теоретической функций распределения используются эмпирические и теоретические частости, которые имеются в распечатке результататов расчета. Поскольку фун­кция распределения представляет собой накопленные частости, фор-мулы для расчета эмпирической F_э(y_j) и теоретической F(y_j) фун­кций распределения имеют вид:

где m_i/n - эмпирические частости; P_i - теоретические час­тости; y_j - правая граница j -гo интервала; k-число интервалов. Значения y_j определя-ются на основании значений середин интерва­лов, приведенных в распечатке.

Для каждого y_j вычисляется модуль разности между эмпирической и теоретической функциями распределения АВS(F_э(у_j) - F(y_j)).

Результаты расчетов следует свести в таблицу 1.

Таблица 1

Данные для проверки гипотезы по критерию Колмогорова

Интервалы значений случайной величины [y(j-i),yj[	Эмпири- ческие частос- ти mj/n	Теорети- ческие частости Pj	Эмпиричес- кая функ- ция Fэ(yj)	Теорети- ческая функция F(yj)	ABS(Fэ(yj)-F(yj))

Из последнего столбца таблицы выбирается наибольший модуль разности между эмпирической и теоретической функциями распреде­ления

D = max ABS(F_э(y_j)-F(y_j)) , j = l...k.

Вычисляется значение критерия Колмогорова

При заданном уровне значимости по таблице определяют гранич­ное значение LAMBDA(alfa), проверяют условие LAMBDA < LAMBDA(alfa) и делают соответствующий вывод о согласовании, теоретического и эмпирического распределений.

Необходимо помнить, что для проверки гипотезы используют те значения критериев и те теоретические частости, которые были полу­чены для заданного теоретического закона распределения.

5. Содержание отчета