2. Построение математических моделей

2.1. Детерминированные модели

2.1.1. Решение систем линейных уравнений

Исходный вид системы:

a_{1 1} x_{1 + ... +} a_{1 i} x_{i + ... +} a_{1 p} x_{p =} b₁

_{. . .}

a _{j 1} x_{1 + ... +} a _{j i} x_{i + ... +} a _{j p} x_{p =} b_j

_{. . .}

a _{p 1} x_{1 + ... +} a_{p i} x_{i + ... +} a_{p p} x_{p =} b_p

где a _{i j} – коэффициенты системы при неизвестных; b_i – свободные члены.

В свернутом виде система описывается следующим выражением:

; , .

В матричном виде система имеет вид

А Х = В,

a_{1 1} ... a_{1 i} ... a_{1 p}

. . .

где А = a_{j 1} ... a_{j i} ... a_{j p}

. . .

a _{p 1}... a _{p i}... a _{p p}

b₁

. . .

B = b_j

. . .

b_p

х₁

. . .

Х = х_j

. . .

х_p

Требуется найти значения Х, удовлетворяющие всем уравнениям системы.

Методами решения систем линейных уравнений являются: метод подстановок, метод последовательного исключения переменных, метод Крамера (матричный метод). Могут также применяться методы решения систем нелинейных уравнений.

Метод подстановок (последовательного выражения переменной из одного уравнения и подстановки в другое) не удобен для алгоритмизации расчетов при переменном числе переменных.

Метод последовательного исключения переменных достаточно удобен для машинной реализации. При этом методе с помощью преобразований строк текущей системы (выравнивания коэффициентов при первой переменной текущей системы и взаимного вычитания из одного уравнения другого) получается новая система без первой переменной. Таким образом, на каждом этапе таких последовательных преобразований получаем понижение числа переменных (на последнем этапе до одной):

a_{1 1} x_{1 + ... +} a_{1 i} x_{i + ... +} a_{1 p} x_{p =} b₁

a'_{2 2} x_{1 + ... +} a'_{2 i} x_{i + ... +} a'_{2 p} x_{p =}b'₂

. . .

х_р = b'_р ,

где штрихом обозначены значения коэффициентов после преобразований.

Значение свободного члена для уравнения с одной переменной дает решение, например по переменной х_р (х_р=b'_р), Затем из одного из уравнений системы предпоследнего этапа находится х_р-1 и т.д., для 1-го – x₂ и из исходной системы – х₁. Разновидность – метод Гаусса с выбором главного элемента.

Метод Крамера основан на матричном исчислении и наиболее удобен с точки зрения соста вления алгоритма и его программной реализации на компьютере.

По методу Крамера

X = A^-1 B

или

x_i = det A_i / det A ,

где А ^-1 – матрица, обратная матрице А;

A_i – матрица, полученная по матрице А с заменой в ней i- го столбца столбцом свободных членов (a_ji=b_j), ;

det – детерминант (определитель) матрицы.

Если det A равен нулю, то система не определена. При малых значениях det A система слабо обусловлена.

2.1.2. Решение систем нелинейных уравнений

Задача состоит в нахождении корней следующей системы уравнений

f _i(X) = 0 }, ,

где X = { x₁, x₂,...,x_m}.

Для решения могут применяться следующие методы:

метод простых итераций;

метод Зейделя, отличающийся от метода простых итераций тем, что уточненные значения x_i сразу подставляются в последующие уравнения;

на основе методов поиска экстремума многомерных функций и др.

Метод простых итераций состоит в реализации процесса по следующей формуле:

x _{i (k+1)} = F_i(X_k),

где F_i(X) = f _i(X) + x _i =x _i;

i – номер переменной;

k – номер итерации.

Итерации выполняются до тех пор, пока сохраняется хотя бы по одному из x _i условие

abs ( x _i(k+1) - x _i(k) ) > E,

где Е – заданная точность.

Метод обеспечивает сходимость, если F _j(X) / x _i <1, , .

Графическая интепретация метода приведена на рисунке 2.1, а схема алгоритма на рисунке 2.2.

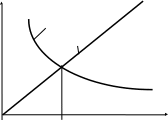
f_i(X)+x_i,

x_i f_i(X)+x_i

x_i

x_рi x_i

Рисунок 2.1 – Графическая интерпретация метода простых итераций (x_рi – решение)

Решение с применением методов поиска экстремума (оптимизации) многопараметрических функций основано на том, что формируются функции вида

или (*)

(**)

где f _i(X)=0 , .

Сходимость в большой степени определяется тем методом, который будет применен для поиска минимума функции Z. Для решения системы уравнений минимальное значение функции Z должно быть равно нулю. Это условие является необходимым и достаточным. Если Z не равно нулю, то это указывает или на отсутствие решения или на неэффективный метод поиска минимума. При применении свертывания уравнений в функцию по (*) быстрее сходимость и ниже точность решения, а для функции (**) наоборот.

1

Пуск

2

Ввод m, E , m – число переменных и уравнений

x( i ), E – точность поиска

x(i)– начальные (текущие) приближения Х

3

F(i)=f_i(X)+ x( i )

для i от 1 до m

4

L=1 L – признак окончания расчетов

5

6 Нет

abs(F(i)-x(i))>E

Да

7

L = 0

8

x(i) = F(i)

Нет 9 10

L = 1 Да Вывод x(i),

11 Рисунок 2.2 – Схема алгоритма

Останов метода простых итераций