Способ 5

Критерий Z_о является минимальным (максимальным) из частных критериев z_i (частные критерии должны быть одной размерности и вида экстремума)

или

.

Для придания гибкости этому способу можно использовать весовые коэффициенты k_i при z_i. Изменяя набор k_i, можно определять необходимые цели.

Способ 6

Критерий Z_о является одним из множества частных критериев z_i (главным), отвечающим основной цели. По остальным критериям может проверяться выполнение наложенных на них ограничений.

Для логических критериев в зависимости от поставленной конечной цели возможны следующие способы их объединения:

цель достигается при выполнении всех целей одновременно

(конъюнкция критериев);

цель достигается при достижении хотя бы одной частной цели

(дизъюнкция критериев),

1.4. Принятие решений в условиях риска и неопределенности

Задача в условиях риска состоит в том, что из-за случайности влияния отдельных факторов, например, внешней среды, с каждой принимаемой стратегией Х_i связано множество возможных результатов Y_j с известными вероятностями p(Y_j,X_i), , . При этом достигается эффект V(Y_j, X_i).

Обобщенной оценкой стратегии X_i является величина ожидаемого эффекта V_o(X_i), рассчитываемая по формуле .

Если в качестве исходных параметров известны вероятности различных состояний среды, то обобщенная оценка V_o(X_i) стратегии X_i определяется по формуле:

,

где R – общее число возможных состояний внешней cреды; p(U_r)– вероятность нахождения внешней среды в состоянии U_r ( ); V(X_i,U_r) – эффект, который складывается при стратегии X_i и состоянии среды U_r.

Принятие решений в условиях риска состоит в определении оптимальной стратегии X_i как

,

где V_o(X_i) – оценки эффективности (полезности) для стратегий X_i, .

При принятии решений в условиях неопределенности информация о состоянии внешней среды (природы) неизвестна принимающему решение (наблюдателю).

Относительно состояния среды наблюдатель может высказывать определенные гипотезы. Такие предположения о вероятном состоянии среды называется субъективными вероятностями p(U_r), . В этом случае имеет место задача принятия решений в условиях риска.

В условиях неопределенности вероятности возможных состояний среды неизвестны. Для выбора оптимальной стратегии в условиях неопределенности предложен ряд критериев.

Критерий Вальда (критерий "осторожного наблюдателя") основывается на предположении, что среда будет находиться в неблагоприятном состоянии, и имеет решающее правило

.

Критерий Гурвица основывается на следующем решающем правиле:

,

где k_d – коэффициент доверия.

По нему предполагается, что среда находится с вероятностью k_d в благоприятном состоянии и с 1 – k_d – в неблагоприятном. При k_d = 0 получаем критерий Вальда, а при k_d = 1

– стратегия "здорового оптимиста".

Критерий Лапласа (случай предположения о равновероятных состояниях среды) P(U₁)=P(U₂)=... =P(U_R) имеет решающее правило

.

Критерий Сэвиджа (критерий минимизации "сожалений") основывается на расчете "сожалений" , равных полезности результата при данном состоянии среды U_r относительно наилучшего решения в зависимости от стратегии X_i, определяемого как :

.

К рассчитанным сожалениям применяется решающее правило

.

Этот критерий минимизирует возможные потери при условии, что состояние среды неблагоприятное.

Выбор одного из вышеуказанных критериев в качестве решающего производится принимающим решение.

Пример.

Организации необходимо принять решение относительно наиболее эффективного числа машиномест на проектируемой платной автомобильной стоянке. Ожидаемая прибыль V(X_i,U_r) в зависимости от числа мест X_i и состояния среды (числа занятых мест) U_r приведена в таблице. В этой же таблице приведены вероятности возможных состояний среды P(U_r).

Xi	V(Xi , U r) и Vs(Xi , U r) (выделенные курсивом) при Ur / P(Ur)
	150/0.1	200/0.1	250/0.6	300/0.2
200	-15	30	30	30
	0	0	-20	-30
250	-35	20	50	50
	-20	-15	0	-15
300	-55	-10	45	60
	-40	-40	-5	0

Решение.

Критерий Вальда

По этому критерию от строительства следует отказаться, так как при оптимальной стратегии имеет место отрицательный эффект.

Критерий Гурвица при K_d =0.6

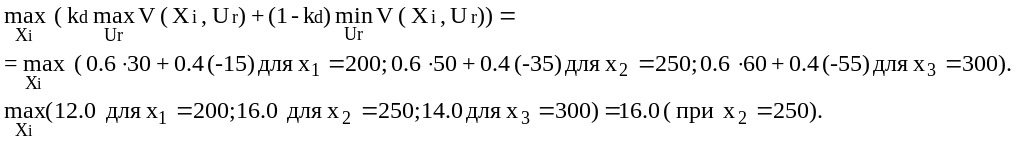и при Kd =1.0

Критерий Лапласа

Критерий Сэвиджа

Результаты расчета сожалений по ранее приведенной формуле даны в таблице вторыми строками. Например, для 1-го столбца (U_r=150) сожаления определяются по выражению

По рассчитанным сожалениям поиск оптимального решения проводится следующим образом

Если известны вероятности состояния среды, то решение производится в условиях риска:

Для условий примера по большинству критериев наиболее эффективно строительство стоянки на 250 машино-мест.

Пример компьютерной программы для принятия решений в условиях риска и неопределенности приведен в приложении 1.