3.8. Эвристические методы решения транспортных задач

Эвристические методы – это приближенные методы решения оптимизационных задач, позволяющие принимать рациональные решения. Преимуществом таких методов является ускорение получения решения с одновременным учетом всех установленных ограничений.

Такие методы применяются для решения:

транспортной задачи линейного программирования – метод Фогеля;

маршрутизации перевозок ресурсов мелкими отправками по сборочно-развозочным маршрутам – метод на основе кратчайшей связывающей сети, метод на основе расчета выигрышей (метод Кларка-Райта) или метод на основе решения задачи о коммивояжере;

маршрутизации перевозок ресурсов помашинными отправками – метод "гарантированного эффекта" и методы на основе расчета выигрышей.

3.8.1. Маршрутизация перемещения ресурсов помашинными отправками

Метод гарантированного эффекта основывается на формировании множества замкнутых маршрутов из отдельных перевозок (ездок), удовлетворяющих установленным ограничениям (по числу ездок, длине, времени на движение и т.п.) и следующему условию

,

где l_гi – длина (стоимость) i –й производительной ездки;

l_хj – длина (стоимость) j –й непроизводительной ездки;

m – число производительных ездок;

n – число непроизводительных ездок;

K_г – коэффициент гарантированного эффекта.

Большие значения K_г принимаются при местных перевозках (порядка 1,15) и меньшие при магистральных перевозках (порядка 1,05).

Из множества образованных возможных рациональных маршрутов включаются в окончательное решение маршруты по максимуму значений Z. При этом на принятом к включению в решение маршруте осваиваются при отдельных ездках объемы перевозок ресурса, удовлетворяющие условию ,

где Q_i – объем ресурса при i-й перевозке (с учетом ранее окончательно принятых маршрутов);

Q_mi – объем ресурса i-й перевозки, включенный в данный маршрут;

γ_сi – коэффициент использования вместимости транспортных средств при i-й перевозке.

Если объем какой-то перевозки освоен полностью, то все рациональные маршруты, не включенные в окончательное решение и содержащие такую перевозку, исключаются из дальнейшего рассмотрения. Если перевозка или ее часть не входит ни в один из окончательно принятых рациональных маршрутов, то она осваивается на маятниковом маршруте с обратным непроизводительным пробегом.

Например, требуется решить задачу маршрутизации для исходных данных, приведенных на нижеследующей схеме (рисунок 3.25).

Из схемы следует, что возможен маршрут А-В-С-Д-А с Z= (11+10) – 1.15 (6.0+5.0) = 4.9 >0(при K_г =1.15) .

Если принять, что дополнительных ограничений нет, то этот маршрут вводится в окончательное решение с объемом перевозок , т.е. при 1-й ездке назначается объем 100 и при 2-й ездке 100*0.8=80.

Объем 2-й перевозки ресурса в объеме 20 ед. (остаток от осваиваемого на принятом маршруте) назначается на маятниковый маршрут с обратным непроизводительным пробегом.

А 11 км Q₁=100 γ_с1 =1.0

В

8км

6км

Д C

10 км Q₂=100 γ_с2 =0.8

Рисунок 3.25 – Пример схемы транспортной сети и корреспонденций ресурса

Метод на основе расчета выигрышей предусматривает определение значений сокращения пробега (стоимости, времени на проезд и т.п.) для всех возможных вариантов объединений исходных перевозок (ездок) по две или по две и по три (объединение большего числа ездок практически не применяется).

Выигрыш от объединения определяется как разница между производительным и непроизводительным пробегом на маршруте . Например, при рассмотрении объединения по две перевозки выигрыши рассчитываются по формуле (см. рисунок 3.26): .

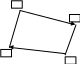i

j

n

k

Рисунок 3.26 – Схема транспортной сети и корреспонденций ресурса (перевозок)

В качестве критерия очередности включения объединенных маршрутов в окончательное решение может приниматься максимум выигрыша , а также другие измерители. Например, в качестве такого критерия могут применяться:

максимум коэффициента использования пробега

или максимум отношения производительных пробегов к непроизводительным

или минимум отношения непроизводительных пробегов к общим (коэффициент непроизводительных пробегов)

или минимум отношения непроизводительных пробегов к производительным

.

Рекомендуется принимать рациональные маршруты со значениями коэффициента использования пробега β не ниже 0.55-0.60 (меньшие допускаемые значения соответствуют магистральным и большие местным перевозкам) и минимальными значениями z_но порядка 0.40-0.45 (большие допускаемые значения соответствуют магистральным и меньшие местным перевозкам).

Порядок окончательного формирования системы маршрутов для освоения перемещения ресурсов соответствует ранее приведенному для метода гарантированного эффекта.