2) Статистическое имитационное моделирование
Статистическое имитационное моделирование основывается на генерации случайных величин, имитации функционирования системы и статистической обработке результатов моделирования. Методом моделирования может быть исследована СМО любой степени сложности.
Для проведения моделирования могут использоваться как универсальные языки программирования так и проблемно-ориентированные - GPSS, SIMULA и др.
Параметры функционирования системы оцениваются при моделировании по результатам многократного обслуживания требований (многократных испытаний). При имитации работы системы случайные величины (длительность обслуживания в каналах, интервалы между поступлениями требований, время возврата требований в систему, моменты возникновения отказов каналов и их длительность и др.) получают генерацией по ранее приведенным алгоритмам в зависимости от вида распределения (закон, усечение, смещение).
Число обслуживаний (опытов) необходимо принимать таким, чтобы обеспечить оценку интересующих параметров с заданной точностью при принятой доверительной вероятности.
Таким образом, определение числа опытов производится по аналогии с расчетом размера выборки для исследования случайных величин. При этом это число рекомендуется определять в ходе моделирования на основе оценки точности рассчитываемых параметров.
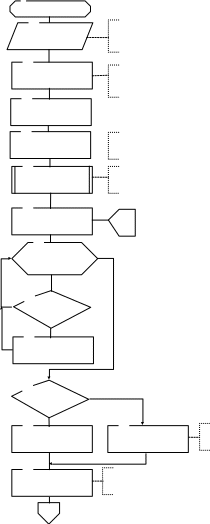
Алгоритмы моделирования ранее рассмотренных систем массового обслуживания приведены на рисунках 2.18 и 2.19. Число моделируемых обслуживаний определяется на основе формулы для нормального закона распределения, а в качестве интересующего показателя принята средняя продолжительность ожидания требованием начала обслуживания. Отноcительная точность оценивания задана равной с односторонней доверительной вероятностью = 0.95 (квантиль равна 1.645).
Структура алгоритмов следующая:
блок 2– ввод и вывод на принтер исходных данных;
блоки 3-6 – формирование начальных условий моделирования;
блоки 7-10 – поиск канала (источника) с минимальным значением момента времени освобождения от предыдущего обслуживания (прибытия на обслуживание);
блоки 11-18– имитация обслуживания требований и накопление сумм длительностей времени простоев и обслуживания;
блоки 19-21– принятие решения об окончании моделирования или его продолжении;
блок 22 – наращивание номера опыта (испытания);
блоки 23-24 – вычисление средних значений параметров и вывод их на монитор (принтер).
1
Пуск
2 n – число каналов; No – минимальное число испытаний; tобс – средняя
Ввод n,No, tобс, L , длительность времени обслуживания; L – средняя интенсивность
потока на обслуживание; – относительная точность оценки продолжи-
тельности простоев требований в очереди
3 S1,S2,S3 –суммы длительностей простоев требований в
S1=0 : S2=0 очереди, простоев каналов, обслуживания требований
S3=0 : S4=0 S4– сумма квадратов длительностей простоев требований в очереди
4
j=1
5
To =0 To – текущий момент прибытия требования для j-го обслуживания
6
Tпi=0, Tпi – текущий момент освобождения i-го канала от обслуживания
7
k=1 22
8
Нет 9
Tпi < Tпk
Да
10
k = i
11
Нет
To < Tпk
Да
12 13
t1 = Tпk - To t2 = To - Tпk t1 и t2 – соответственно продолжитель-
t2 =0 : S1=S1+t1 t1 =0 : S2=S2+t2 ность простоя требования и канала
в ожидании начала обслуживания
14 toбсм – продолжительность обслуживания при j - м опыте
toбсм = - tобс ln 1 1 – псевдослучайное число в интервале [0.-1.0] 1-й после-
довательности
15
14
15
tин = -1/L ln 2 tин – интервал времени прибытия очередного требования на обслуживание
2 – псевдослучайное число в интервале [0.-1.0] 2- й последовательности
16
tk = tk + t2 + toбсм tk = To + t1 + toбсм
17
To = To + tин
18
S3=S3+tобсм
S4=S4+t21
7
19 Нет
j >No
22
Да j=j+1
20
I =( S4 j/S21-1)1.6452/2
21
j > I Нет
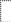
Да
23 tот и tок – соответственно средняя продолжитель-
tот=S1/j: tок=S2/j ность ожидания требованиями и каналами начала
tобо=S3/j обслуживания; tобо – средняя продолжительность
обслуживания по результатам моделирования
24
Вывод n, L, toбс,
j, toт, toк, toбo,
25
Останов
Рисунок 2.18 – Алгоритм моделирования многоканальной СМО разомкнутого типа с ожиданием
1
Пуск
2 m– число источников; No – миним. число испытаний; tобс –
Ввод m,No, tобс , 1 , средняя длительность времени обслуживания; 1 – поток,
генерируемый одним источником; – относительная
точность оценки продолжительности простоев требований в очереди
3
S1=0 : S2=0 S1,S2,S3 –суммы длительностей простоев требований в
S3=0 : S4=0 очереди, простоев каналов, обслуживания требований
S4– сумма квадратов длительностей простоев требований
4 в очереди
j=1
5
To =0 Tо – текущий момент осбождения канала от обслуживания
6
Tтi=0, Tтi– текущий момент поступления требования от i-го источника
7
k=1 22
8
Нет 9
Tтi < Tтk
10 Да
k = i
11
To < Tтk
12 13 t1 и t2 – соответственно продолжитель-
t1 = Tт k - To t2 = To - Tтk ность простоя требования и канала
t2 =0 : S1=S1+t1 t1 =0 : S2=S2+t2 в ожидании начала обслуживания
14 Toбсм – продолжительность обслуживания при j - м опыте
toбсм = - tобс ln 1 1 – псевдослучайное число в интервале [0.-1.0] 1- й после-
довательности
15
14
15
w1 – период времени до следующего возврата в систему
w1 = -1/1 ln 2 2 – псевдослучайное число в интервале [0.-1.0] 2- й после-
довательности
16
Tо= Tтk + t2 + toбсм Tо= Tо + t1 + toбсм
17
Tтк = Tтк + w1
18
S3=S3+tобсм
S4=S4+t21
7
19
j >No Нет 22
j=j+1
20
I =( S4 j/S21-1)1.6452/2
Да
21 Нет
j > I
Да
23 tот и tок – соответственно среднее время ожидания требованиями
tот=S1/j:tок=S2/j и каналом начала обслуживания; tобо – средняя длительность
tобо=S3/j времени обслуживания по результатам моделирования
24
Вывод m, tобс, 1,
j, toт,toк,toбo,
25
Останов
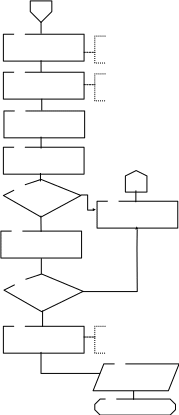
Рисунок 2.19 – Алгоритм моделирования одноканальной СМО замкнутого типа с ожиданием