1) Аналитическое исследование систем массового обслуживания

Многоканальная разомкнутая система массового обслуживания

В качестве примера рассматривается многоканальная СМО с простейшим потоком требований и экспоненциальным распределением времени их обслуживания (рисунок 2.16). Система с ожиданием и без приоритетов требований и каналов друг перед другом.

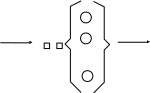
Каналы

1

Очередь 2

Входящий ... Выходящий

поток поток

n

Рисунок 2.16 – Схема многоканальной разомкнутой системы массового обслуживания

Поток требований на обслуживание характеризуется средней интенсивностью L (с^-1, мин^-1, ч^-1 , сут^-1) и имеет пуассоновский закон распределения. Доказано, что в этом случае интервалы между поступлениями требований распределены по экспоненциальному закону распределения. Длительность времени обслуживания требования характеризуется средней величиной t_обс (потоком обслуживания v=1/t_обс). Число каналов в системе – n.

Основные показатели функционирования многоканальной разомкнутой системы массового обслуживания рассчитываются по формулам:

вероятность того, что все каналы обслуживания свободны

,

где x = L t_обс – приведенный поток, физическая сущность которого – число каналов, необходимое для обслуживания требований при детерминированных их потоке и времени обслуживания. Должно соблюдаться условие x < n ;

вероятность того, что в системе находится ровно k требований

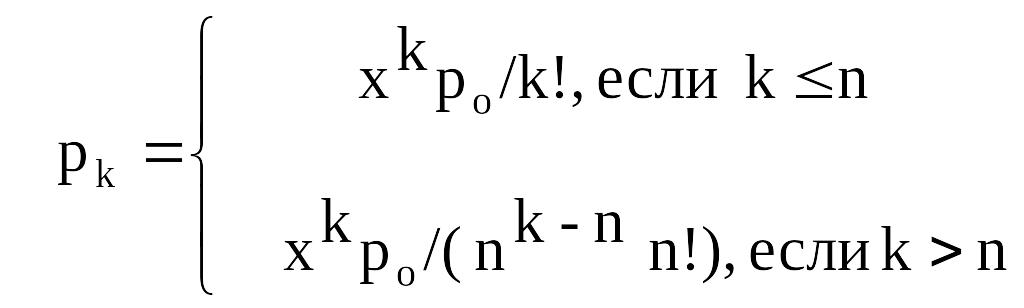
вероятность того, что все каналы заняты

;

вероятность того, что занято ровно n каналов

вероятность того, что время ожидания требованием начала обслуживания t_oж меньше или больше t_з

или

;

среднее число незанятых каналов обслуживания

;

среднее число требований, простаивающих в очереди на обслуживание

;

среднее число требований на обслуживании

;

средняя длительность времени ожидания требованиями начала обслуживания .

Многоканальная замкнутая система массового обслуживания

В качестве примера рассматривается многоканальная СМО с числом каналов n и числом источников, генерирующих требования, m (рисунок 2.17). При этом поток требований, создаваемый одним источником, простейший. Длительность времени обслуживания требований в канале имеет экспоненциальное распределение. Система с ожиданием и без приоритетов требований и каналов друг перед другом.

Поток требований, генерируемых одним источником во время нахождения его вне системы обслуживания, характеризуется средней интенсивностью λ (с^-1 , мин^-1, ч^-1, сут^-1). Обратная величина λ является средней продолжительностью времени до последующего поступления требования от обслуженного источника (средний период до возврата в систему на обслуживание).

Время обслуживания характеризуется средней величиной t_обс или потоком обслуживания  =1/t_обс.

Основные показатели функционирования многоканальной замкнутой системы массового обслуживания рассчитываются по формулам:

вероятность того, что все каналы обслуживания свободны

;

1 – источники требований

6

Входящий Очередь Выходящий – обслуживающие каналы

поток 2 поток

1

3 4 5 2 … 7

n

m, …

Рисунок 2.17 – Схема многоканальной замкнутой системы массового обслуживания

x= λ t_обс или х= λ/ – приведенный поток от одного источника требований при детерминированных потоке и времени обслуживания;

вероятность того, что в системе обслуживания находится ровно k требований

;

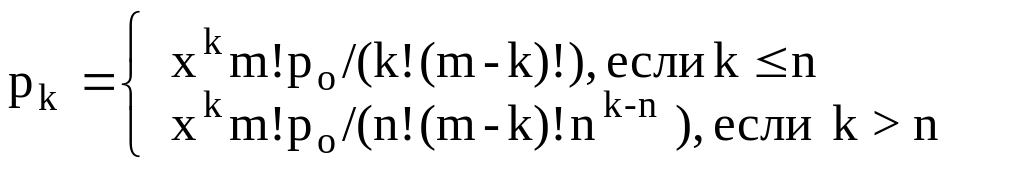среднее число незанятых каналов обслуживания

;

среднее число требований, простаивающих в очереди на обслуживание

;

среднее число требований, находящихся на обслуживании

M_обс = n_з ; n_з = n - n_o.

Для одноканальной замкнутой СМО (n=1) имеют место следующие зависимости:

вероятность того, что все каналы свободны ;

средняя продолжительность ожидания требованием начала его обслуживания t_ожт=t_обс(m/(1-p_o)- 1)-1/х;

средняя продолжительность простоя канала в ожидании очередного требования на обслуживание t_ожк = p_ot_обс /(1-p_o );

вероятность того, что канал занят p_з = 1 - p_о .