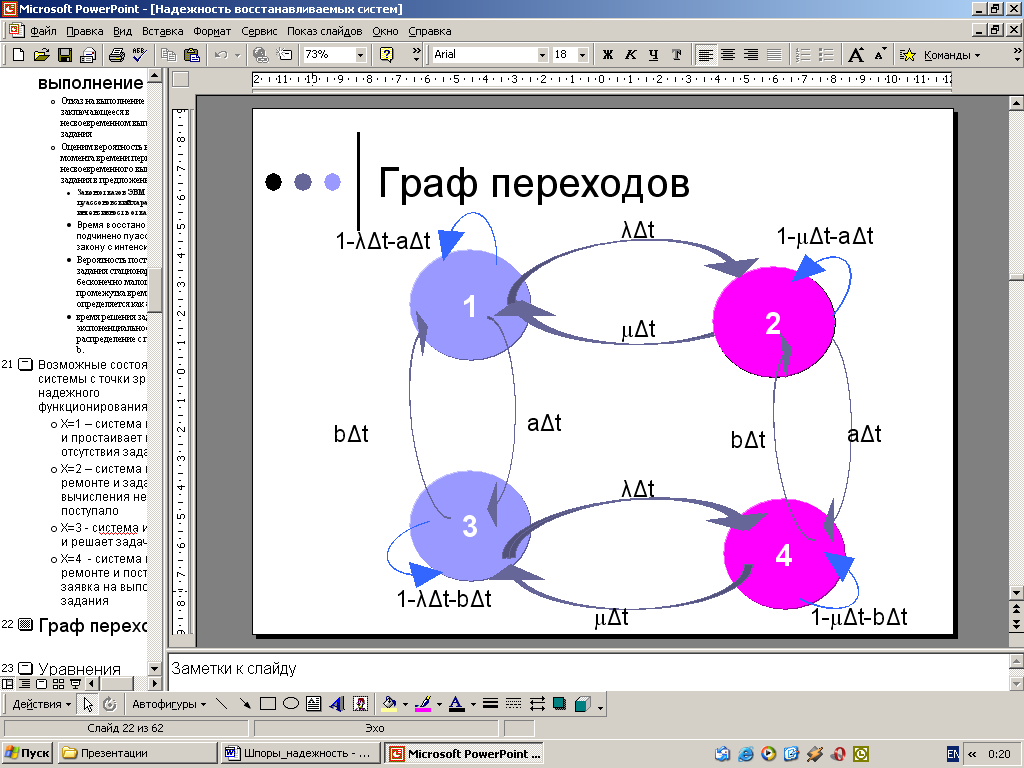
23. Графы и матрицы переходов состояний.

Отказ на выполнение – событие заключающееся в несвоевременном выполнении задания

Оценим вероятность наступления момента времени первого несвоевременного выполнения задания в предложениях

• Закон отказов ЭВМ носит пуассоновский характер, интенсивность отказов равна λ

• Время восстановления подчинено пуассоновскому закону с интенсивностью µ

• Вероятность поступления задания стационарна и для бесконечно малого промежутка времени Δt определяется как аΔt

• время решения задачи имеет экспоненциальное распределение с параметром b.

Возможные состояния системы с точки зрения ее надежного функционирования:

• X=1 – система исправна и простаивает из-за отсутствия задания

• X=2 – система в ремонте и задание на вычисления не поступало

• X=3 – система исправна и решает задачу

• X=4 – система в ремонте и поступила заявка на выполнение задания

Граф переходов:

Уравнения нахождения системы во всех состояниях

Вероятность нахождения системы во всех 4-ех состояниях:

Вероятность невыполнения задания

Марковские процессы дискретные в пространстве и во времени

При изучении сложных систем используются математические модели, основанные на марковских процессах. Основные понятия марковского процесса

• состояние

• переход

Автоматизированные системы управления можно рассматривать как сложные системы, которые в любой момент времени находятся в одном из возможных состояний. Состояние АСУ описывается числом работоспособных элементов.

Если сосредоточить внимание лишь на переходах системы из одного состояния в другое и точно пронумеровать их во времени, то можно представить себе поведение системы как процесс с дискретным временем.

Переход из одного состояния в другое называется шагом процесса. Для простого МП вероятность перехода из состояния x_i в x_j - есть функция только номеров начального и конечного состояний и не зависит от состояния системы до попадания в x_i.

Для описания поведения системы достаточно ввести набор условных вероятностей p_ij того, что осуществится переход из состояния X_i в состояние X_j, и задать исходное состояние, в котором находилась система в начальный момент времени.

Матрица переходов:

Матрица переходных вероятностей должна удовлетворять условиям:

Последнее условие отражает факт, что процесс, находящийся в момент n в состоянии i, перейдет в одно из допустимых состояний в момент n+1 с вероятностью 1.

24. Дискретные в пространстве и времени Марковские процессы

Основные понятия марковского процесса:

• Состояние;

• Переход.

1. АСУ можно рассматривать как сложные системы, которые в любой момент времени находятся в одном из возможных состояний.

2. Состояния АСУ описывается числом работоспособных элементов.

Моделирование поведения системы

Если сосредоточить внимание лишь на переходах системы из одного состояния в другое и точно пронумеровать их во времени, то можно представить себе поведение системы как процесс с дискретным временем.

Переход из одного состояния в другое называется шагом процесса

Для простого МП вероятность перехода из состояния x_i в x_j - есть функция только номеров начального и конечного состояний и не зависит от состояния системы до попадания в x_i.

Для описания поведения системы достаточно ввести набор условных вероятностей p_ij того, что осуществится переход из состояния x_i в состояние x_j, и задать исходное состояние, в котором находилась система в начальный момент времени.

Дискретный вероятностный процесс {x(t),t=0,1,2…} называется марковским, если для любой последовательности моментов времени t₀< t₁< . . . <t_n и для любых чисел x₀, x₁, . . . ,x_n справедливо

P[x(t_n) ≤ x_n|x(t₀)≤ x₀;

x(t₁)≤ x₁;…;x(t_n-1)≤ x_n-1] =P[x(t_n)≤ x_n|x(t_n-1)≤ x_n-1]

Определение дискретного МП

Пусть n=1,2,… - моменты переходов

X(n) – состояния в эти моменты времени

Марковский процесс с дискретным временем определен, если заданы все переходные вероятности p_ij(n,n+1)=p_ij(0,1)=p_ij, то марковский процесс называется стационарным.

Матрица переходов:

Матрица переходов должна удовлетворять условиям:

Последнее условие отражает факт, что процесс, находящийся в момент n в состоянии i, перейдет в одно из допустимых состояний в момент n+1 с вероятностью 1.

Матрицы, обладающие вышеуказанными свойствами – стохастические.