Примеры: Элементарные функции Функция с устранимым разрывом Функция знака Ступенчатая функция

35. Точка   называется точкой разрыва функции  , если она определена в некоторой проколотой окрестности точки   (то есть определена на некотором интервале, для которого   служит внутренней точкой, но в самой точке  , возможно, не определена Классификация точек разрыва функции

Все точки разрыва функции разделяются на точки разрыва первого и второго рода.  Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке

• Существуют левосторонний предел   и правосторонний предел  ;

• Эти односторонние пределы конечны.

При этом возможно следующие два случая:

• Левосторонний предел и правосторонний предел равны друг другу:

Такая точка называется точкой устранимого разрыва.

• Левосторонний предел и правосторонний предел не равны друг другу:

Такая точка называется точкой конечного разрыва. Модуль разности значений односторонних пределов  называется скачком функции.

36. Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как пределотношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Геометрич смысл

Если функция   имеет конечную производную в точке   то в окрестности   её можно приблизить линейной функцией

Функция   называется касательной к   в точке   Число  является угловым коэффициентом или тангенсом угла наклонакасательной прямой.

Механич смысл Скорость изменения функции

Пусть   — закон прямолинейного движения. Тогда   выражает мгновенную скорость движения в момент времени   Вторая производная   выражает мгновенное ускорение в момент времени 

Вообще производная функции   в точке   выражает скорость изменения функции в точке  , то есть скорость протекания процесса, описанного зависимостью 

37. Производная суммы (разности) функций

Производная алгебраической суммы функций выражается следующей теоремой.

Производная суммы (разности) двух дифференцируемых функций равна сумме (разности) производных этих функций:

Производная конечной алгебраической суммы дифференцируемых функций равна такой же алгебраической сумме производных слагаемых. Например,

Производная произведения функций.

Пусть u(x) и u(x) - дифференцируемые функции. Тогда произведение функций u(x)v(x) также дифференцируемо и

Производная произведения двух функций не равана произведению производных этих функций.

Производная частного функций.

Пусть u(x) и u(x) - дифференцируемые функции. Тогда, если v(x) ≠ 0, то производная частного этих функций вычисляется по формуле

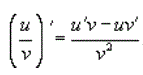
38. Пусть   - функция от аргумента x в некотором интервале  . Если в уравнении   y считать аргументом, а x - функцией, то возникает новая функция  , где   - функция обратная данной. Пусть     - функция, дифференцируемая в точке   ,    - функция, дифференцируемая в точке    , причем   . Тогда    - сложная функция независимого переменного  , дифференцируема в точке     и ее производная в этой точке вычисляется по формуле    .

39. Теорема 12. Пусть функция x = φ(t) имеет обратную функцию t = Ф(x). Если функцииx=φ(t), y = ψ(t) дифференцируемы и φ'(t) ≠ 0, тогда

40. Логарифмическим дифференцированием называется метод дифференцирования функций, при котором сначала находится логарифм функции, а затем вычисляется производная от него. Такой прием позволяет эффективно вычислять производные степенных и рациональных функций.  41. Производные высших порядков

  Ясно, что производная

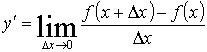
функции y =f (x) есть также функция от x:

y' =f ' (x)

.   Если функция f ' (x) дифференцируема, то её производная обозначается символом y'' =f '' (x) и называется второй производной функции f(x) или производной функции f(x) второго порядка. Пользуясь обозначением

можем написать

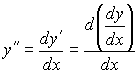
Пример.    

  Очень удобно пользоваться также обозначением

 ,

указывающим, что функция y=f(x) была продифференцирована по x два раза.   Производная второй производной, т.е. функции y''=f '' (x) , называется третьей производной функцииy=f(x) или производной функции f(x) третьего порядка и обозначается символами

.

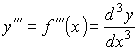  Вообще n-я производная или производная n-го порядка функции y=f(x) обозначается символами

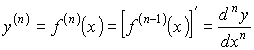
42. Дифференциалом функции у=ƒ(х) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dу (или dƒ(х)) Дифференциал функции f(x) в точке x₀ равен приращению, которое получает ордината касательной к кривой y =f(x) с абсциссой в точке x₀ при переходе из точки касания в точку с абсциссой x₀+Δx.

43. Если вещественная функция, непрерывная на отрезке   и дифференцируемая на интервале  , принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производная функции равна нулю. Для любой функции  , аналитической в некоторой односвязной области   и для любой замкнутой кривой  справедливо соотношение  .

44.