22. Пара́бола (греч. Παραβολή — приложение) — геометрическое место точек, равноудалённых от данной прямой (называемой директрисойпараболы) и данной точки (называемой фокусом параболы).

23. 1. Уравнение плоскости по точке и нормальному вектору. Если плоскость проходит через точку M₀(x₀,y₀,z₀) и перпендикулярна к вектору  =(A,B,C), то ее уравнение записывается в виде: A(x-x₀)+B(y-y₀)+C(z-z₀)=0

2. Уравнение плоскости в «отрезках». Если плоскость пересекает оси координат O_x, O_y, O_z в точках M₁(a,0,0) M₂(0,b,0) M₃(0,0,c) соответственно, то ее уравнение можно записать в виде:   (16)  где a≠0, b≠0, c≠0

3. Уравнение плоскости по трем точкам. Если плоскость проходит через точки M_i(x_i,y_i,z_i (i=1,3), не лежащие на одной прямой, то ее уравнение можно записать в виде:

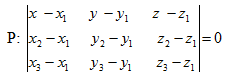 (17)

24. 1. D = 0, Ax+By+Cz = 0 - плоскость проходит через начало координат.

2. C = 0, Ax+By+D = 0 - плоскость параллельна оси Oz.

3. C = D = 0, Ax +By = 0 - плоскость проходит через ось Oz.

4. B = C = 0, Ax + D = 0 - плоскость параллельна плоскости Oyz.

25. Множество и элемент множества относятся к числу первичных понятий, для которых несуществует определений в строгом смысле слова. Поэтому обычно говорят о множестве как о наборе предметов ( элементов множества ), наделённых определёнными общими свойствами. Множество книг в библиотеке, множество автомобилей на стоянке, множество звёзд на небосводе, растительный и животный мир Земли – всё это примеры множеств.

 

Конечное множество состоит из конечного числа элементов, например, множество страниц в книге, множество учеников в школе и т.д.

 

Пустое множество (   ) не содержит ни одного элемента, например, множество крылатых слонов, множество корней уравнения  sin x = 2  и т.д.

 

Бесконечное множество состоит из бесконечного числа элементов, т.е. это множество, которое неявляется ни конечным, ни пустым. Примеры: множество действительных чисел, множество точекплоскости, множество атомов во Вселенной и т.д.

 

Счётное множество – множество, элементы которого можно пронумеровать. Например, множества натуральных, чётных, нечётных чисел. Счётное множество может быть конечным (множество книг в библиотеке ) или бесконечным ( множество целых чисел, его элементы можно пронумеровать следующим образом:

 

элементы множества:    …, –5,   – 4,   –3,   –2,   –1,   0,   1,   2,   3,   4,   5, …

 

номера элементов:           ...   11       9      7      5      3    1    2    4    6    8   10 ...  ) .

 

Несчётное множество – множество, элементы которого невозможно пронумеровать. Например, множество действительных чисел. Несчётное множество может быть только бесконечным (продумайте, почему ? ).

 

Выпуклое  множество – множество, которое наряду с любыми двумя точками А и В содержит также весь отрезок  АВ. Примеры выпуклых множеств: прямая, плоскость, круг. Однако, окружностьне является выпуклым множеством.

 

Способы задания множеств. Множество может быть задано следующим образом:

 

– перечислением всех его элементов по их названиям ( так описываются множество книг в библиотеке, множество учеников в классе, алфавит любого языка и т.д.);

 

– заданием общей характеристики ( общих свойств ) элементов данного множества ( например, множество рациональных чисел, собаки, семейство кошачих и т.д.);

 

– формальным законом построения элементов множества ( например, формула общего члена числовой последовательности, Периодическая система элементов Менделеева и т.д.).

26. Функция (отображение, оператор, преобразование) — математическоепонятие, отражающее связь между элементами множеств. Табличный способ. Довольно распространенный, заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством. Графический способ. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению. Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим Словесный способ. Этот способ состоит в том, что функциональная зависимость выражается словами. 1) Область определения функции и область значений функции.

Область определения функции - это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена. Область значений функции - это множество всех действительных значений y, которые принимает функция.

В элементарной математике изучаются функции только на множестве действительных чисел.

2) Нули функции.

Нуль функции – такое значение аргумента, при котором значение функции равно нулю.

3) Промежутки знакопостоянства функции.

Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.

4) Монотонность функции.

Возрастающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.

Убывающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.

5) Четность (нечетность) функции.

Четная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат.

Нечетная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = - f(x). График нечетной функции симметричен относительно начала координат.

6) Ограниченная и неограниченная функции.

Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x . Если такого числа не существует, то функция - неограниченная.

7) Периодическость функции.

Функция f(x) - периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими. (Тригонометрические формулы).

27. Обра́тная фу́нкция — функция, обращающая зависимость, выражаемую данной функцией. Сложная функция – функция от функции. Элементарные функции — функции, которые можно получить с помощью конечного числа арифметических действий икомпозиций из следующих основных элементарных функций:

• алгебраические:

  • степенная;

  • рациональная.

• трансцендентные:

  • показательная и логарифмическая;

  • тригонометрические и обратные тригонометрические.