2.Умножение

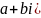* =( * ) =ac+adi+bic+bd =(ac-bd)+(ad+bc)i

Свойства умножения:

1.Ассоциативно

2.Коммуникативно

3.Роль нейтрального будет играть 1=1+0i

4. = = 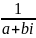= = 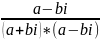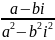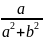+ 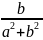i

3.Деление

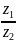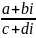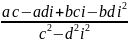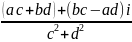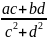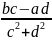= = = = = + i

Поле комплексных чисел.

Множество всех комплексных чисел относительно сложения и умножения образуют поле.

Поле – это множество с операциями сложения и умножения обладающими свойствами коммуникативности, ассоциативности, наличие нейтрального элемента и поглощающего элемента для каждого элемента.

(В случаи «+» - поглощающий – противоположный; в случаи «-» - поглощающий – обратный) обе операции связаны законом дистрибутивности.

Вопрос 14.

Геометрическая интерпретация комплексных чисел, модуль и аргумент комплексного числа. Сопряженные комплексные числа. Свойства сопряженных комплексных чисел. Решение квадратных уравнений в поле комплексных чисел.

Геометрическая интерпретация комплексных чисел, модуль и аргумент комплексного числа.

Как известно, действительные числа можно изображать точкам числовой прямой. При этом каждому действительному числу соответствует единственная точка числовой прямой. Верно и обратное утверждение: каждой точке числовой прямой соответствует единичное действительное число. Значит, между точками числовой прямой и множеством всех действительных чисел установлено однозначное соответствие.

Комплексные числа можно изобразить геометрически точками плоскости. Каждому комплексному числу поставили в соответствии точку плоскости с координатами А(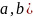

Ось ОХ – действительная ось

Ось ОУ – мнимая ось

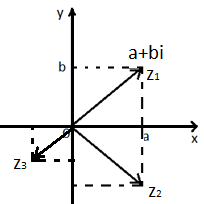
Комплексные числа изобращаются (.) плоскасти или радиус векторами.

Длина радиуса вектора комплексного числа z, называется модулем комплексного числа.

Угол поворота радиуса вектора к положительному направлению оси ОХ, называется аргументом комплексного числа.

Argz – аргумент

Сопряженные комплексные числа. Свойства сопряженных комплексных чисел.

Сопряженным комплексным числом z, z=a+bi, называется 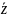(zс чертой) =a-bi

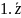= z

2. * z=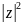

3.z€Ri(a=0) => = -z

4.z€R(b=0) => = z

5. = +

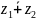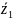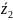
6. = -

7. = *

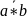8. =

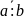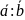
9.f(z)= * + * + * +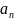

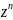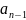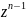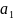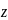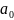
10. =

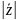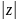
11.arg =- argz

12. f( )=

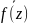
Вопрос 15.

Тригонометрическая форма комплексного числа. Переход из алгебраической формы в тригонометрическую и из тригонометрической в алгебраическую.

Комплексное число в тригонометрической форме имеет вид

r-модуль комплексного числа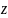

φ - arg

Если дано комплексное число в алгебраической форме, ,то его можно изобразить на плоскости с помощью радиус вектора в точке A(a,b)

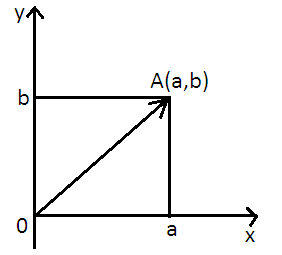
Так как это длина радиус вектора, то =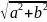 , а аргумент находится следующим образом:

Переход из алгебраической формы в тригонометрическую и из тригонометрической в алгебраическую.

Чтоб перейти от тригонометрической форме к алгебраической, достаточно просто раскрыть скобки и привести подобные.

=

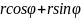
a€R b€R

Чтоб перейти от алгебраической к геометрической:

1.Находим модуль комплексного числа по формуле =

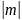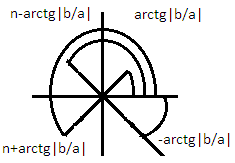
2.По знакам a и b определяем четверть, в которой расположено данное число

Пример

1.z=1

Z+0i=1(cos0+i*sin0)=cos0+i*sin0

4.z=-2+3i

= =

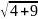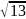
φ=n-arctg|-3/2| = n-arctg|3/2|

=(cos(n-arctg(3/2))+i*sin(n-arctg(3/2)))