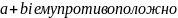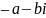Вопрос 12.

Понятие множества, операции над множествами. Бинарная алгебраическая операция, примеры. Определение группы, кольца, поля, примеры.

- Множество – это объединение элементов по некоторому определенному признаку. Признак определяется заранее.

Во множестве не требуется понятия порядка, в нем нет отношения «>» и «<». Не сравниваем.

- множество называется пустым, если оно не содержит ни одного элемента.

- если каждый элемент множества А является элементом множества В, то А называется подмножество В, или А содержится в В.

- Множество содержащее все рассматриваемые множества – называется универсальным.

Операции над множествами.

Операции над множествами – это способы получения новых множеств

1)Перечисление множеств.

А В – множество элементов € и А и В.

2)Объединение множеств

АuВ- множеством элементов, принадлежащих хотя бы одному множеству А и В.

3)Разность множеств

А\В – множество элементов, принадлежащих А и не принадлежащих В.

4)Пусть И - универсальное множество, A содержится И, тогда все элементы принадлежащие И, но не принадлежащие А образуют множества называемые дополнением к множеству А.

Бинарная алгебраическая операция, примеры

Вопрос 13.

Понятие мнимой единицы и необходимость её введения. Степени мнимой единицы. Комплексные числа в алгебраической форме. Действия над комплексными числами в алгебраической форме, свойства операций, поле комплексных чисел.

Круги Эйлера

N - Натуральные числа

Z – Целые числа

Q – Рациональные числа

R – Действительные числа

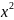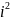Во множестве действительных чисел не имеют решения простейшие квадратные уравнения, например, +1=0. Математики пришли к необходимости расширить понятия числа, чтобы в новом множестве можно было всегда извлечь квадратный корень. Новое множество назвали множеством комплексных чисел, введя понятие мнимой единицы: =-1

Степени мнимой единицы.

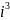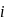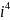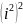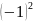=-1

= * =-

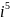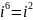= = = 1

= * =

* =-1

= * =-

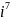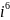Комплексные числа в алгебраической форме.

- Комплексным числом называется формальное выражение a+bi, где a и b действительные числа, =-1.

Запись комплексного числа z в виде z=a+bi называется алгебраической формой. При этом a называется действительной частью, а b – мнимой частью числа z. Используются обозначения: a=Rez, b=lmz (1. от фр. действительный и 2 мнимый)

Множество всех комплексных чисел обозначим буквой С. Таким образом, по определению, имеем: С=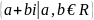

- Два комплексных числа a+bi и с+di будем считать равными, если равны их действительные и мнимые части:

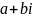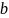=с+di <=> a=с и =d

– Два числа с+di и число с-di называется сопряженным комплексным числом

Действия над комплексными числами в алгебраической форме.

1.Сложение

=

=

=(

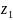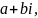
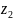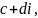
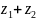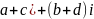
Свойства сложения:

1.сложение коммуникативно

2.ассоциативно

3.Роль нейтрального играет 0

4.