Вопрос 9.
Определитель матрицы. Определитель 2-гои 3-го порядка. Решение системы линейных уравнений методом Крамера.
Членом определителя называется произведение элементов определителя взятых по одному из каждой строки и каждого столбца.
Определителем квадратной матрицы называется сумма всех членов определителя с их знаками.
Он равен сумме произведений элементов некоторой её строки на их алгебраическое дополнение.
Определитель 2-го порядка.
=
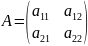
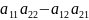
Определитель 3-го порядка.
= =
Решение системы линейных уравнений методом Крамера.
A=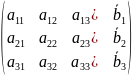
=
=
=
=
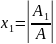
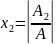
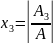
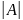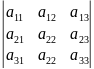
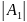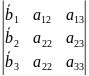
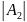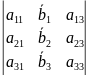
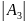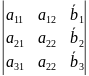
Вопрос 10. Определитель n-го порядка, свойства определителя. Вычисление приведением к треугольному виду.
Определитель n-го порядка.
Пусть дана квадратная матрица порядка n.
. Определителем квадратной матрицы А порядка n называется сумма произведений элементов этой матрицы, взятых по одному из каждой строки и каждого столбца, причем произведение берется со знаком, равный знаку подстановки, первая строчка которой составлена из индексов строк элементов.
Свойства определителя.
1.Определитель не измениться, если его строки заменить столбцами и наоборот замена строк столбцами называется транспонированием.
2.При перестановке двух строк (столбцов) определитель меняет знак на противоположный.
3.Определитель имеющий 2 одинаковые строки (столбца) =0
4.Если в матрице все элементы некоторой строки (столбца) равны = 0, то определитель этой матрицы также = 0.
5.Если каждый элемент некоторой строки (столбца) матрицы умножить на число k то определитель этой матрицы увеличиться в k раз.
6.Если в матрице две строки пропорциональны т определитель этой матрицы = 0.
7.Определитель произведения матриц равен произведению определителей.
8.Определитель матриц не изменится, если к элементам одной строки (столбца) прибавить соответствующие элементы другой строки (столбца) умноженные на любое число.
9. Если квадратные матрицы А и В имеют одинаковый порядок (n) и кроме одной i-той строки имеют одинаковые элементы на одинаковых местах т.е. отличаются только одной строкой то сумма определителе этих матриц равна определителю у которой все элементы кроме i-той строки совпадают с элементами матриц А и В, а в i-той строке стоит сумма элементов i-той матриц А и В.
Вычисление приведением к треугольному виду.
Часто удобно вычислять определитель матрицы приведением её к ступенчатому виду. Если при этом в матрице появляется нулевая строка, то определитель матрицы = 0.Если же такого не происходит, то ступенчатая матрица имеет треугольный вид и её определитель = произведению элементов, стоящих на главной диагонали.
Вопрос 11.
Понятие минора и алгебраического дополнения элемента. Вычисление определителей с помощью алгебраических дополнений элементов строки и столбца.
Минором
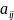матрица A n-го порядка называется
определитель n-го порядка матрица
полученная из матрицы вычеркиванием
i-той
строки и j-того
столбца (т.е. вычеркиваем строчку и
столбец в котором стоит данный элемент
)
A=
=
=
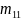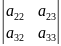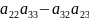
- алгебраическое дополнение матрицы А называется его минор взятый со знаком
«+» если (i+j) четная
«-» если (i+j) не четная
Обозначается
=
*
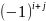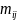
A=
=
=
(11вопрос)Вычисление определителей с помощью алгебраических дополнений элементов строки и столбца.
Определитель квадратной матрицы = сумме произведений элементов некоторой её строки или столбца на их алгебраическое дополнение.
A=
=
=
=