
- •Вопрос 1.
- •Вопрос 2.
- •Вопрос 3.
- •Вопрос 4.
- •Вопрос 5.
- •Вопрос 6.
- •Вопрос 7.
- •Вопрос 8.
- •Вопрос 9.
- •Вопрос 10. Определитель n-го порядка, свойства определителя. Вычисление приведением к треугольному виду.
- •Вопрос 11.
- •Вопрос 12.
- •Вопрос 13.
- •1.Сложение
- •2.Умножение
- •3.Деление
- •Вопрос 14.
- •Вопрос 15.
- •Вопрос16. Умножение и деление комплексных чисел в тригонометрической форме(формулы с доказательством). Формула Муавра.
- •1.Умножение.
- •2.Деление.
- •3.Возведение в степень.
- •Вопрос 17.
- •Вопрос 18.
Вопрос 5.
Линейная комбинация векторов. Линейно зависимая и линейно независимая система векторов, основные свойства линейной зависимости с доказательством. Примеры линейно зависимых и линейно независимых систем векторов.
-
Линейной
комбинацией
вектора в такой, что при некоторых
значений чисел
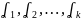
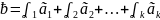
(под n-ой комбинацией будем понимать сумму векторов с их коэффициентами, в конечном итоге получим вектор)
Пример:

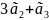
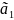 (1;-1;4;0)
(1;-1;4;0)
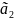 (-1;0;3;6)
(-1;0;3;6)
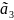 (8;7;6;5)
(8;7;6;5)
2(1;-1;4;0) - 3(-1;0;3;6) + (8;7;6;5) = (13;5;5;-13)
- линейная комбинация называется тривиальной, если все её коэффициенты = о и не тривиальной если хотя бы один из коэффициентов отличный от нуля.
– система
векторов
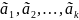 называется линейно зависимой, если
существует, не тривиальна линейная
комбинация данных векторов, равна нуль
вектору, т.е. если существует числа
такие что
называется линейно зависимой, если
существует, не тривиальна линейная
комбинация данных векторов, равна нуль
вектору, т.е. если существует числа
такие что
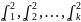 ≠
0 (что хотя бы одно из
≠
0 (что хотя бы одно из
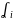 ≠0)
≠0)
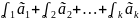 =
Ō
=
Ō
(1;1;1;1)
(1;-1;2;3)
(3;-1;5;7)
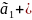
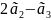 =
Ō – нетривиальная линейная комбинация
= Ō=>
=
Ō – нетривиальная линейная комбинация
= Ō=>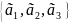 - линейно
зависимая система
- линейно
зависимая система
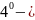 система
векторов
называется линейно
независимой,
если только тривиальная ей линейная
комбинация будет =
Ō вектору. Т.е. существует ни нулевого
набора коэффициента
такого, что
=
Ō
система
векторов
называется линейно
независимой,
если только тривиальная ей линейная
комбинация будет =
Ō вектору. Т.е. существует ни нулевого
набора коэффициента
такого, что
=
Ō
Т.е эта система векторов не является, линейно зависимой.
Основные свойства линейной зависимости.
– если система векторов содержит нулевой вектор, то она линейно зависимая
Док-во:
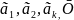
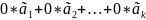 *
ʆ * Ō = Ō
*
ʆ * Ō = Ō
![]() ʆ≠0
ʆ≠0
Ō
Нетривиальная линейная комбинация, но равная Ō => значит она линейна зависимая
-
если некоторая часть конечной системы
часть конечной системы линейно зависима,
то и вся система линейно – зависима
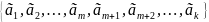
k>m
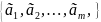 -линейно
зависимая подсистема =>
-линейно
зависимая подсистема =>
Существует
набор чисел
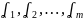 среди которых есть хотя бы один отличный
от нуля такой, что
≠
0;
среди которых есть хотя бы один отличный
от нуля такой, что
≠
0;
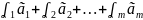 =
Ō.
=
Ō.
Тогда можно составить нетривиальную линейную комбинацию для всей системы векторов равную Ō – вектору
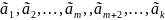
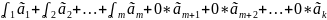 =
Ō =>
=
Ō =>
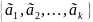 -
линейно зависимая
-
линейно зависимая
- (необходимое и достаточное условие линейной зависимости системы векторов или признак линейной зависимости) Конечная система векторов содержащая более одного вектора линейно зависима <=> когда она содержит вектор являющийся линейной комбинацией остальных векторов системы (можно считать данную формулировку за определения линейной зависимости)
Вопрос 6.
Основная теорема о линейной зависимости и следствие из неё. Базис и ранг системы векторов.
Теорема
Если
система векторов
 )линейно
выражается через систему векторов
)линейно
выражается через систему векторов
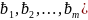 2),
k>m
то система (1) линейно зависима, если
длинная система линейно выражается
через короткую, то длинная система
линейно зависима.
2),
k>m
то система (1) линейно зависима, если
длинная система линейно выражается
через короткую, то длинная система
линейно зависима.
Система векторов линейно выражается через другую систему векторов, если вектор (1) системы можно представить как линейную комбинацию векторов (2) системы.
Док-во:
Составим линейную комбинацию векторов системы (1)
=
Ō(3) в силу условия каждый вектор
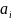 - можно представить в виде линейной
комбинации векторов системы(2)
- можно представить в виде линейной
комбинации векторов системы(2)
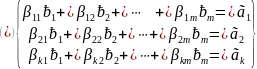
Подставим выражение для векторов из системы (*) линейную комбинацию (3)
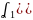 )
+
)
+
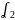 (
(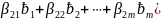 +
+
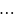 +
+
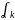 (
(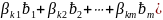 = Ō
= Ō
Раскроем
скобки и приведем подобные относительно
вектора
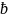
 )
)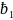 + (
+ (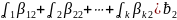 +
+ (
+
+ (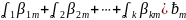 =
Ō
=
Ō
Одним из решений для набора коэффициентов в данном равенстве является нулевое решение (так как система (2)может быть и линейно зависимой и линейно независимой, то нас устроит любой набор коэффициентов в данном равенстве, лишь бы он было верным)
(Возьмем самый простой вариант – когда все коэффициенты = 0) получим следующую систему линейных уравнений относительно неизвестных
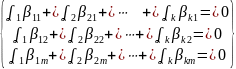
Данная система однородная т.е. всегда совместна (есть решение) в этой системе m-уравнений и k – неизвестных. По условию k> m => число неизвестных больше числа уравнений, а значит данная система не определена т.е. имеет и не нулевое решение. А значит, существует не нулевой набор коэффициентов такой, что выполняется равенство (3), а значит система (1) линейно зависима.
Следствие 1.
В арифметическом n – мерном векторном пространстве всякая система векторов содержащая более чем n – векторов линейно зависима.
Док-во
– существует
линейно не зависимая система состоящая
из единичных векторов
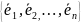
Е
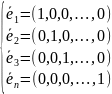
И каждый вектор пространства может быть представлен в виде линейной комбинации единичных векторов.
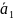 =
(
=
=
(
=

Таким
образом любой вектор системы
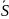 =
=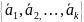
k>n
€ – можно представить в виде линейной комбинации единичных векторов т.е. система S линейно выражается через систему E – при этом система S длиннее системы Е, а значит система S линейно зависима.
Следствие 2
Если
система
- линейно не зависима и линейно выражается
через систему
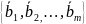
k≤m
Док-во
От противного.
Если предположим, что k>m,т.е. первая система векторов «длиннее» второй, то по предыдущей теореме первая система должна быть линейно зависимой, что противоречит условию
Следствие 3.
В арифметическом n – мерном векторном пространстве любая линейно независимая система векторов содержит не более, чем n – векторов.
Док-во.
Предположим противное, приходим к противоречию со следствием 2.
(6 вопрос)Базис и ранг системы векторов.
Дана система векторов S
– базисом непустого множества векторов S называется такая её линейно независимая подсистема, через которую линейно выражается любой вектор данной системы.
Теорема
Если система векторов S содержит не нулевой вектор, то она имеет базис. Любые два базиса системы S содержат одинаковое количество векторов.
Док-во
1.Докажем что S содержит базис
Пусть
Ō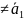 €S=>
€S=>
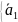 - система из одного не нулевого вектора
линейно независима.
- система из одного не нулевого вектора
линейно независима.
Если
всякий вектор система S
можно выразить, через
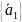 (1),
то система (1) есть базис системы S.
(1),
то система (1) есть базис системы S.
Если
в системе S
найдется вектор
 ,
который не выражается через систему
один, то система
,
который не выражается через систему
один, то система
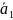 2)
– линейно независима. Если каждый
вектор системы S
линейно выражается через систему (2),
то система 2 – базис.
2)
– линейно независима. Если каждый
вектор системы S
линейно выражается через систему (2),
то система 2 – базис.
Если
существует в системе вектор
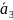 ,
который не выражается через систему
(2), то система
,
который не выражается через систему
(2), то система
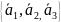 (3)
и т.д.
(3)
и т.д.
Рассуждение: продолжаем до тех пор пока не получим подсистему - линейно независимую и через которую выражается любой вектор данной системы, такая подсистема и будет базисом системы S.
2.Докажем что любые 2 базиса содержат одинаковое количество векторов.
Т= ≤S
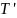 =
=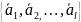 ≤S
≤S
И Т и являются базисам S
k=l
Т
– базис S,
то все векторы
линейно выражаются через Т
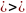 (по
следствию теоремы 1) => т.к.
- линейна независима и выражается чрез
другую, то l≤k
(по
следствию теоремы 1) => т.к.
- линейна независима и выражается чрез
другую, то l≤k
Обратно, т.к. - базис, то Т – линейно выражается через значит k≤l
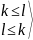 l=k
l=k
Ранг матрицы
рангом системы векторов называется количество векторов в любом базисе данной системы
Дана матрица
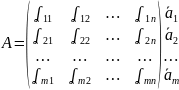
Строки данной матрицы можно считать векторами называемыми вектор – строчками данной матрицы
Вектор - строчки:
=(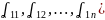
=(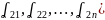
 =(
=(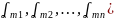
Столбцы данной матрицы можно также считать векторами называемыми вектор – столбцами данной матрицы
Система векторов - столбцами
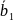 =(
=(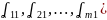
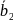 =(
=(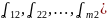
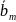 =(
=(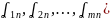
– ранг
система вектор – столбцов матрицы
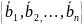 называется столбцовым рангом матрицы
называется столбцовым рангом матрицы
Ранг
системы векторов – строчек матрицы
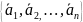 называется строчечным рангом матрицы.
называется строчечным рангом матрицы.
