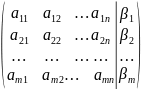Вопрос 1.

Система линейных уравнений: определение, решение, классификация по количеству решения, равносильные системы, элементарные преобразования.

Основные понятия:

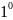- пусть P некоторое числовое множество системой m линейных уравнений с n – неизвестными называется система предложенного вида:

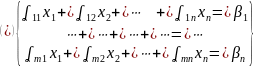
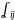€ P первый индекс i – номер строки, второй индекс j – номер переменной.

β € P 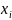- неизвестные

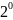- решением СЛУ(*) является набор значений неизвестных

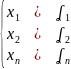
такой что при подстановке в любое другое уравнение (*) будем получать верное числовое равенство.

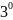– две СЛУ называются эквивалентными (равносильными) если совпадают их множество решений.

Классификация СЛУ

1.Несовместная (не имеет решения)

2.Совмесная (имеет решение)

А) определена (единственное решение)

Б) неопределенна (бесконечное множество решений)

К элементарным преобразованиям СЛУ относятся такие преобразования которые позволяют перейти от данной системы к системе ей равносильной.

1 преобразование – добавление или удаление нулевого уравнения

2 преобразование – умножение любого уравнения системы на число отличное от нуля

3 преобразование – прибавление к любому уравнению системы, любого другого уравнения системы умноженного на некоторое число.

4 перемена двух строк местами.

Вопрос 2.

Ступенчатая СЛУ. Решение и исследование СЛУ методом Гаусса. Матрица, расширенная матрица СЛУ.

– СЛУ называется ступенчатой, если она обладает следующим свойством, если в некотором ее уравнении первый отличный от нуля коэффициент стоит на k-ом месте, то во всех ниже следующих уравнениях (если такие существуют) первый k коэффициент =0 (длина «ступеньки» может быть любой, а высота в один символ)

Теорема: всякую СЛУ путем элементарных преобразований можно привести к ступенчатому виду

Решение методом Гаусса.

Метод Гаусса - заключается в последовательном исключении неизвестных, достигается это следующим образом:

1 сначала СЛУ путем элементарных преобразований СЛУ приводим к ступенчатому виду

До множим первое уравнение на 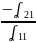первое уравнение прибавим ко второму, затем первое уравнение умножим на 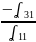прибавим ко второму и тд.

Пока не получим во всех уравнениях начиная со второго нулевые коэффициенты при х, после этого получим систему

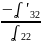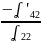Дальше формируем вторую ступеньку для этого второе уравнение полученной системы умноженное на прибавить к третьему уравнению, затем второе уравнение домножаем на , прибавим к четвертому и т.д. Пока не получим нулевые коэффициенты во всех уравнениях начиная с третьего. Аналогично поступаем со всеми первыми (m) – столбцами

2) поднимаясь снизу вверх подстановкой находим значение всех неизвестных начиная с последней, при подстановке происходит последовательное исключение неизвестных из системы начиная с последних.

Исследование СЛУ по её ступенчатому виду.

- если в ступенчатом виде СЛУ имеет число уравнений = числу неизвестных, то система совместна и определена, в этом случае система решается методом Гаусса.

- если в ступенчатом виде СЛУ содержит противоречивое равенство (0=В, где В≠0) то система не совместна.

– Если в ступенчатом виде число уравнений < числа неизвестных, то система совместна и неопределенна.

Матрица, расширенная матрица СЛУ.

Матрицей называется прямоугольная таблица чисел состоящая из m строк содержащих одинаковое количество n элементов.

A =

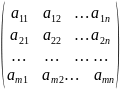
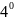Размерностью матрицы А считается количество строк и столбцов ( m*n). Если в матрице А количество строк равно количеству столбцов, то матрицу называют квадратной n. Две матрицы называются равным, если их размерности совпадают и на одинаковых местах стоят равные элементы

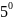Матрицей системы линейных уравнений называют матрицу А, составленная из коэффициентов этой системы; если же к этой матрице приписать столбец свободных членов, то получаем расширенную матрицу В.

В =