Вопрос 15. Конечные разности. Их свойства.

Пусть таблично задана некоторая функция, пусть известны ее значения в некоторых точках.

Определение 1. Конечной разностью первого порядка называется (1)

Определение 2. Конечной разностью второго порядка называется (2)

Определение 3. Конечной разностью n-го порядка называется (3)

Где к=1,2,3…

При этом для полной определенности полагают по определению . Найдем явное выражение конечных разностей через значение функций.

Сравним эти формулы: коэффициенты совпадают.

Свойство: коэффициенты в выражении конечных разностей совпадают с коэффициентами соответствующих разложений биномов ньютона. На практике для вычисления конечных разностей обычно используют таблицы

Вопрос 16. 1 интерполяционный полином Ньютона.

П остановка задачи. На отрезке задано равномерное разбиение т.е дана система равноудаленных точек ; ; в этих точках известны значения функции , вообще говоря сама функция неизвестна. По этим данным требуется построить полином степени не более чем n 1) degre который в узлах принимает те же значения, что и сама функция 2) решение задачи 1)-2) будем искать в следующем виде (6)где - пока неизвестные коэффициенты. Неизвестные коэффициенты будем определять из условия 2) последовательно подстовляя в (6) в узловые точки . 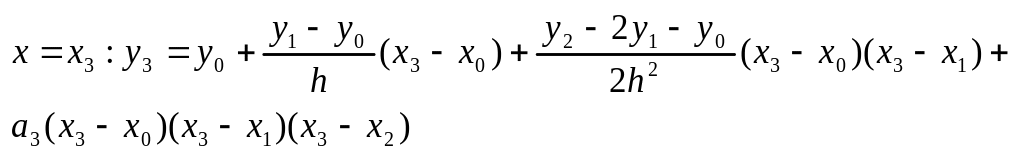учитывая, что узлы равноудалены Подставим в (6)

Этой формулы можно предать более компактный вид или ввести рассмотрение переменную q (10) где формула (10) является предпочтительной когда вычисления проводятся вручную

Замечание №1 Если (близко с порцией точности), то , в таких случаях в формуле (10) можно пренебречь слагаемыми, содержащими , тогда можно пользоваться (11)

Замечание №2: первое ИПН обычно используется для приближенных значениях вычисления функции в начале таблице в первой половине.

Вопрос 17. II интерполяционный полином Ньютона.

Решение задачи будем искать в следующем виде (12) где - пока еще неизвестный коэффициент. Неизвестный коэффициент будем определять из условия (2) последнее подставляем в (12) узловые точки, но не сначала, а с конца.

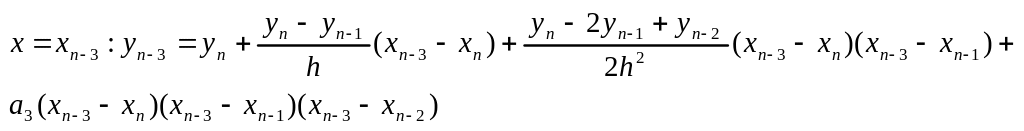
подставим (13) в (12) имеем следующие (14) по аналогии с предыдущими в ведем (15) (16) где

Замечание №3: Если , то , поэтому можно пренебречь слагаемыми, содержащие, , тогда можно пользоваться (17)

Замечание №4 Обычно 2-ой ИПН принимают для приближенных вычислений значения функции в конце таблицы.

Полиномы определяются единственным образом - стандартный вид полинома.

Погрешность приближения функции ИПН. Для оценки погрешности метода использована теорема 2. согласна этой теоремы

Вопрос 18. Интерполяция сплайнами. Кубический сплайны.

При возрастании количество угловых точек возрастает степень интерполяционного полинома. Полином начинает сильно осцеиллировать, это делает их неудобными для вычисления. Высокой степени можно избежать, если ввести в рассмотрение несколько отрезков. которые в объединение дают отрезок и на каждом из них строить интерполяционный полином, однако в этом случае первая производная терпит разрыв ( в точках стыка)

Если узлов n+1, то степень n

Угловые коэффициенты разные , а значит разные и сами производные в этих точках (-слева +справа ) Применение сплайнов избавляет от этого недостатка

Опр1. Сплайном (spline-рейка) называется функция, которая на каждом частичном экспериментальном участке представляет собой алгебраический полином (многочлен), а на всем отрезке непрерывна вместе со своими несколькими производными. Существуют сплайны разных степеней на практике наиболее часто используется кубический сплайн.

Кубический сплайн.

Отрезок [a;b] разобьем на n – равных частей точками x; , где выберем произвольный элемент участок кроме непрерывности самой функции будем требовать непрерывности первой и второй производной

- многочлен, соответствующий участку (1) здесь a_i, b_i, c_i, d_i – пока еще неизвестные коэффициенты (имеем 4n неизвестных коэффициента) Для определения неизвестных коэффициентов будем накладывать условия относительно сплайнов

П ервая группа условий I) потребуем совпадения значения сплайнов и значения функции ; эти условия позволяют нам получить 2n уравнения относительно неизвестных коэффициентов ; подставим уравнение II потребуем непрерывности внутренней узловой точке всего внутри узловых точек(n-1) т.е будем накладывать следующего условия , 2(n-1) –число, полученное уравнение с помощью следующего условий выражение сплайна для этого участка

Найдем производные от и от , (4) (5)

(6) (7) производная справа слева производная справа т.о Аналогично, вторые производные Производные слева производные справа т.о перепишем полученное уравнение 4n-2 –уравнения, а неизвестное 4n.

Не хватает еще 2х уравнений для получения полностью замкнутой системы. Для получения этих уравнений обычно используют условия на концах отрезках [a;b] т.е . Можно ставить различные условия для получения недостающих уравнений, обычно используют следующие условие 1) требования нулевой кривизны в точках a и b. Это условие влечет равенство нулю второй производной в точках a и b 2) первая производная принимает определенное значение в точках a и b 3) вторая производная имеет на концах определенное но не нулевые значения в точках a,b. 4) условие периодичности т.е в точка a,b сплайн принимает одинаковые значения. Получим дополнительное уравнение на основе первого условия производная справная