
- •Вопрос 1. Численное решение нелинейных уравнений. Два этапа поиска корней уравнения. Графический способ отделения корней уравнения.
- •Вопрос 2. Аналитический способ отделения корней уравнения.
- •Вопрос 3. Методы уточнения корней нелинейных уравнений. Метод половинного деления.
- •Вопрос 4. Метод хорд.
- •Вопрос 5. Метод касательных (Ньютона).
- •Вопрос 6. Комбинированный метод хорд и касательных.
- •Вопрос 7. Метод итераций.
- •Вопрос 8. Системы нелинейных уравнений. Метод Ньютона.
- •Вопрос 9. Системы нелинейных уравнений. Метод итераций.
- •Вопрос 10. Системы линейных алгебраических уравнений (слау). Прямые итерационные методы решения слау.
- •Вопрос 11.Слау с трехдиагональной матрицей. Метод прогонки.
- •Вопрос 12. Решение слау методом итераций. Условия сходимости.
- •Вопрос 13. Решение слау методом Зейделя. Условия сходимости.
- •Вопрос 14. Интерполирование функции. Интерполяционный полином Лагранжа.
- •Вопрос 15. Конечные разности. Их свойства.
- •Вопрос 16. 1 интерполяционный полином Ньютона.
- •Вопрос 17. II интерполяционный полином Ньютона.
- •Вопрос 18. Интерполяция сплайнами. Кубический сплайны.
- •Вопрос 19. Обработка экспериментальных данных. Этапы решения задачи.
- •Вопрос 20. Метод наименьших квадратов (мнк).
- •21. Линейное приближение квадратов по мнк.
- •Вопрос 22. Квадратичное приближение квадратов по мнк.
- •Вопрос 23. Полиномиальная аппроксимация по мнк.
- •Вопрос 24. Численное дифференцирование. Формула численного дифференцирования, основанная на применении интерполяционного полинома Ньютона.
- •Вопрос 25.Численное дифференцирование. Метод неопределенных коэффициентов.
- •Вопрос 26. Формула численного дифференцирования, основанные на применении интерполяционных формулах Лагранжа.
- •Вопрос 27.Численное интегрирование. Метод прямоугольников.
- •Вопрос 28. Численное интегрирование. Метод трапеций.
- •Вопрос 29. Численное интегрирование. Метод парабол.
- •Вопрос 30. Квадратурные формулы Ньютона-Котеса.
- •Вопрос 31. Задача Коши для обыкновенного дифференциального уравнения (оду) I порядка. Метод Эйлера.
- •Вопрос 32. Численное решение задачи Коши для оду I порядка методом Рунге-Кутта.
- •Вопрос 33. Система оду I порядка. Метод Эйлера.
- •Вопрос 34. Система оду I порядка. Метод Рунге-Кутта.
- •Вопрос 35. Конечно—разностный метод решения дифференциальных уравнений. Способы аппроксимации производных.
- •Вопрос 36. Краевая задача для линейного обыкновенного дифференциального уравнения II порядка. Построение конечно-разностной схемы.
- •Вопрос 37. Первая краевая задача для уравнения теплопроводности. Явная конечно-разностная схема.
- •Вопрос 39. Задача Дирихле для уравнения Лапласа. L- сторона квадрата, известна. В задаче Дирихле ставится граничное условие граничное условие 1-го рода. Где - известная функция
Вопрос 10. Системы линейных алгебраических уравнений (слау). Прямые итерационные методы решения слау.
Пусть дана система из n линейных уравнений с n независимыми
![]() Введем в рассмотрение
квадратную матрицу А
Введем в рассмотрение
квадратную матрицу А![]()
![]() .
Тогда система (1) Может быть записана в
матричной форме
.
Тогда система (1) Может быть записана в
матричной форме
![]() Необходимые
и достаточные условия существования и
единственности решения системы линейных
уравнений
Необходимые
и достаточные условия существования и
единственности решения системы линейных
уравнений
![]() определитель
det(А)
определитель
det(А)![]() (2).
Существующий метод решения СЛАУ условно
можно разделить на две большие группы
(2).
Существующий метод решения СЛАУ условно
можно разделить на две большие группы
1)Прямые методы (точные методы)
2)Итерационные методы
1)Прямые методы. Прямые методы позволяют найти решение системы в виде точных формул относительно коэффициентов исходной системы, поэтому такие методы называют ещё точными однако на практике точные решения получаются редко. Это связано с погрешностями округления. Прямые методы достаточно универсальны и применяются для решения линейных систем, возникающих на практике. Представители первой группы: Метод Гауса метод Крамера, метод прогонки.
2) Итерационные методы.
При
использовании итерационного метода
вычисления организуются следующим
образом: сначала создается такое
начальное приближение или начальный
вектор
,
затем используется один шаг алгоритмов
методов находят следующее приближение
затем
к полученному приближению опять применяют
алгоритм методов, находят
![]() ,
таким образом, вычисления продолжают
до тех пор пока не будут найдены 2
приближения
,
,
таким образом, вычисления продолжают
до тех пор пока не будут найдены 2
приближения
,![]() ,
Совпадающие в определенном смысле. При
достижении заданной точности за решение
принимают последнее приближение
,
Совпадающие в определенном смысле. При
достижении заданной точности за решение
принимают последнее приближение
![]() .
Итерационные методы обладают Хорошим
свойством. Свойством Самоисправляемости
. Некоторые представители: метод
итерационный, метод Зэйделя, метод
релаксации,…
.
Итерационные методы обладают Хорошим
свойством. Свойством Самоисправляемости
. Некоторые представители: метод
итерационный, метод Зэйделя, метод
релаксации,…
Матрицы с диагональным преобладанием.
Пусть
дана Квадратичная матрица состоящая
из n-строк
и n
столбцов, Введем в рассмотрение![]() .
Определение- Говорят что матрица А
является матрицей с диагональным
преобладанием если величины ri>0(i=1,n)
Другими словами для такой матрицы
диагональный элемент
.
Определение- Говорят что матрица А
является матрицей с диагональным
преобладанием если величины ri>0(i=1,n)
Другими словами для такой матрицы
диагональный элемент
![]() по
модулю превышает сумму других модулей
не диагональных элементов. Утверждение
Матрица с диагональным преобладанием
не выражена (ее определитель не равен
0) Доказательство: Докажем методом от
противного пусть матрица А имеет
Диагональное преобладание и ее
определитель равен 0 тогда система имеет
не нулевое решение
по
модулю превышает сумму других модулей
не диагональных элементов. Утверждение
Матрица с диагональным преобладанием
не выражена (ее определитель не равен
0) Доказательство: Докажем методом от
противного пусть матрица А имеет
Диагональное преобладание и ее
определитель равен 0 тогда система имеет
не нулевое решение![]() т.е.
вектор
содержит не нулевые компоненты. Т.е.
существует хi
не равное 0. Пусть хк
такое,
что
т.е.
вектор
содержит не нулевые компоненты. Т.е.
существует хi
не равное 0. Пусть хк
такое,
что
![]() .
Рассмотрим к-ую строку или к-ое уравнение
системы (5)
.
Рассмотрим к-ую строку или к-ое уравнение
системы (5)![]() выразим
из этого уравнения к-ое слагаемое через
все остальные
выразим
из этого уравнения к-ое слагаемое через
все остальные![]()
![]() Разделим
на xk
Разделим
на xk
![]() ,
а это противоречит тому что матрица А
имеет диагональное преобладание чтд.
,
а это противоречит тому что матрица А
имеет диагональное преобладание чтд.![]() -
закон контрпозиции.
-
закон контрпозиции.
Прямые методы решения СЛАУ Метод Гаусса
М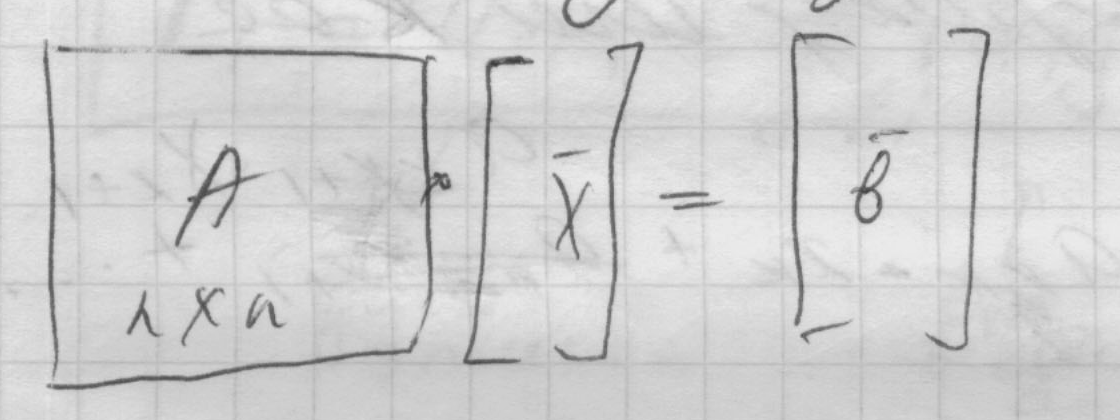 етод
состоит из прямого хода и обратного.
етод
состоит из прямого хода и обратного.
Задача прямого хода приведение матрицы системы к треугольному виду, ниже главной диагонали нули.

В приобразованой системе содержится в последнем лишь одно неизвестное хn
Вопрос 11.Слау с трехдиагональной матрицей. Метод прогонки.
Рассмотрим
системы из n
линейных уравнений с 3-х диагональной
матрицей
![]() матрица
этой системы является трехдиагональной
матрица
этой системы является трехдиагональной

Такие
системы уравнения часто возникают при
решении различных прикладных задач, а
так же при численном решении дифференциальных
уравнений. Для решения таких систем
применяется метод прогонок; он является
модификацией метода Гаусса по аналогии
с методом Гаусса состоит из прямого
хода и обратного. Прямой ход называется
прямой прогонкой. Задача прямой прогонки
выражение каждого хi
через последующие
![]() .
Pi,
Qi
–называют прогоночными коэффициентами.
Задача – прохождение (n-1)
пара прогонного коэффициента. Выведем
формулы для нахождения этих коэффициентов.
Из этого уравнения системы (7) Выразим
x1
через x2
.
Pi,
Qi
–называют прогоночными коэффициентами.
Задача – прохождение (n-1)
пара прогонного коэффициента. Выведем
формулы для нахождения этих коэффициентов.
Из этого уравнения системы (7) Выразим
x1
через x2
![]() Запишем
уравнение (8) При i=1
Запишем
уравнение (8) При i=1
![]() (10)
сравнивая (9) и (10) получаем
(10)
сравнивая (9) и (10) получаем
![]() (11)
(11)
Из (2)
система (7) выразим x2
через x3
используя при этом уравнение (10)![]()
![]()
![]()
Запишем
уравнение (8) при i
= 2
![]()
![]() (12)
рассуждая аналитическим образом легко
вывести формулы для произвольной i-ой
пары.
(12)
рассуждая аналитическим образом легко
вывести формулы для произвольной i-ой
пары.
![]() (13)
(13)
![]() задача обратной прогонки- нахождение
всех неизвестных. Сначала найдем xn,
для этого используем последнее уравнение
исходной системы и уравнение (8) при i=
n-1
задача обратной прогонки- нахождение
всех неизвестных. Сначала найдем xn,
для этого используем последнее уравнение
исходной системы и уравнение (8) при i=
n-1
![]() где
где
![]() -
известно уже.
-
известно уже.
![]()
![]()
![]() (14)
Остальные неизвестные определяются
последовательно по формуле (8) используя
значения ранние найденных прогонычных
коэффициентов
(14)
Остальные неизвестные определяются
последовательно по формуле (8) используя
значения ранние найденных прогонычных
коэффициентов
 Рассмотренный
вариант метода называют еще скалярной
прогонкой существует модификации метода
прогонки. Имеется вариант для решения
системы трехточечных векторных уравнений
эту модификацию называют методом
матричной прогонки.
Рассмотренный
вариант метода называют еще скалярной
прогонкой существует модификации метода
прогонки. Имеется вариант для решения
системы трехточечных векторных уравнений
эту модификацию называют методом
матричной прогонки.
