Вопрос 6. Комбинированный метод хорд и касательных.

Допустим что корни уравнения f(x) =0(1) определен и лежит на , х* .

Комбинированный метод состоит в совместном применении 2-х методов хорд и касательных.

Геометрическая иллюстрация.

Где выполняется

и т.д. до тех пор пока не будет определен [α_n;β_n], длинна которого . При выполнении этого условия вычисления прекращают и за решение принимают среднюю точку последнего отрезка. . Так как и в методе хорд теоретически возможны 4 случая; расчетных формул 2 пары . В случае 1;4 т.е. в точке β знак функции совпадает со знаком вогнутости, метод касательных справа, хорды слева. В формуле (из )

в случае 2;3 анологичные условия имеют место для конца α. метод касательных слева, метод хорд справа.

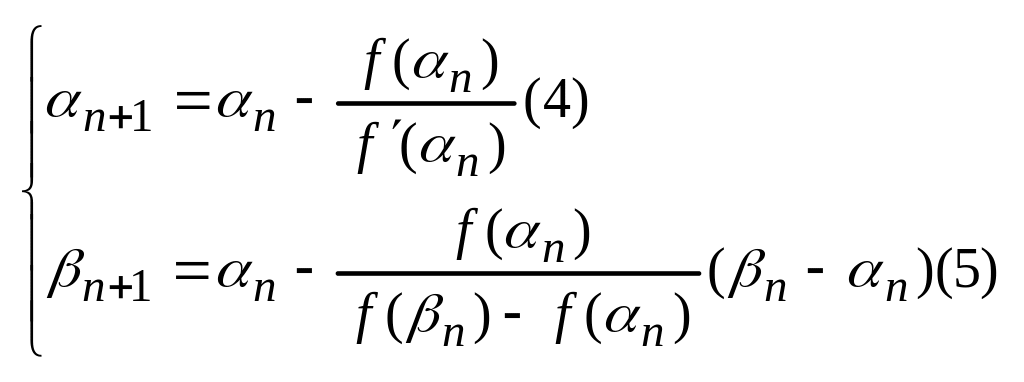
В случае 2;3 используют формулы (4)(5). В выбранной серии формул (2),(3),(4),(5) n=1,2,3,….. Вычисления по выбранной формуле продолжаются до выполнения условия (6) . При выполнении условия (6) вычисления прекращаются и за корень уравнения принимают середину последнего участка

Вопрос 7. Метод итераций.

f(x) =0(1) х* .

Исходное уравнение приведем к виду :

. Выберем начальное приближение x₀ х₀ подставим в правую часть уравнения (2), полученное возьмем за х_{1 .} Произвольное n-ое приближение (3) n=1,2,3,….

Теорема 2. Если выполняется следующие условия

1)Функция определена и дифиренциируема на ;

2)для всех x из :

3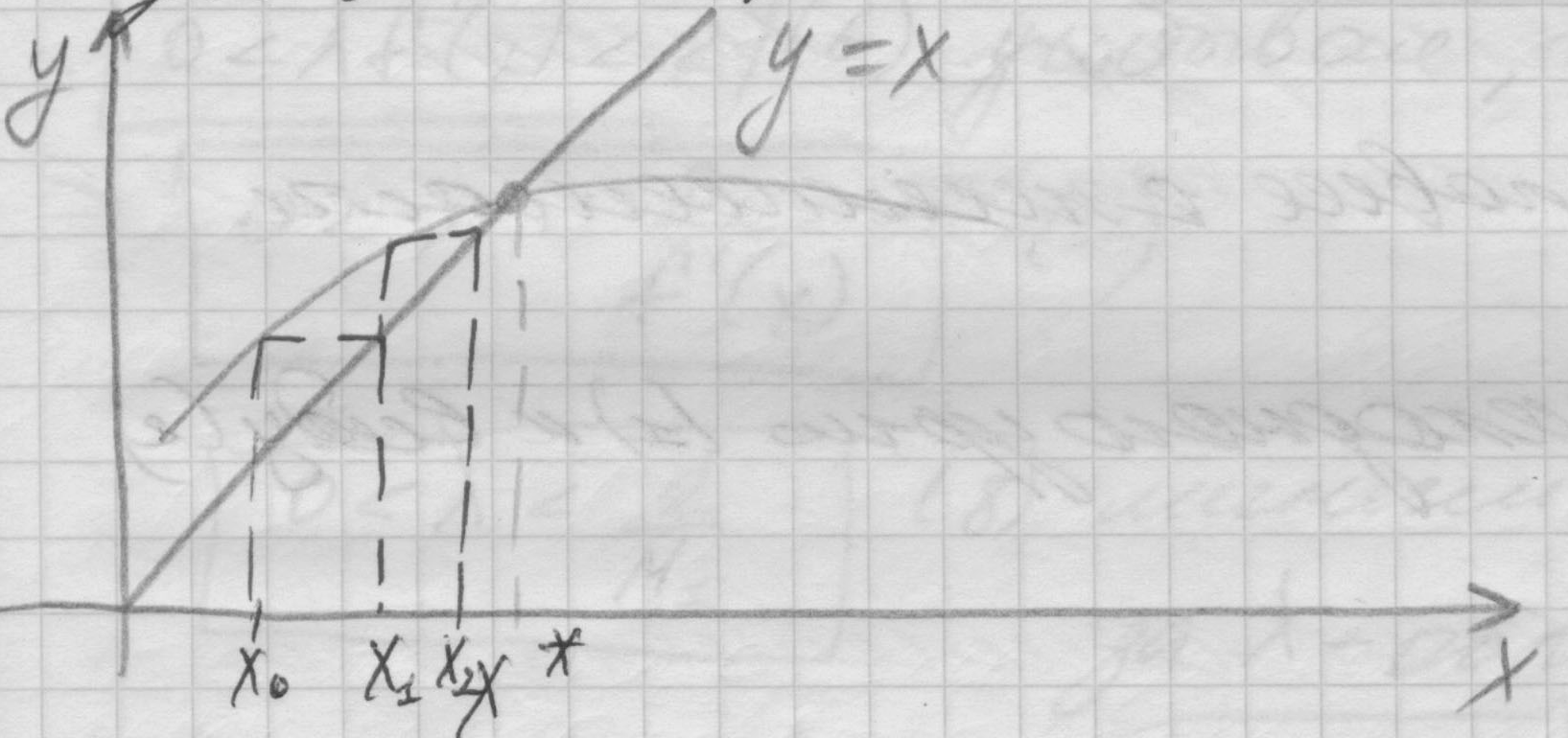 ) существует q(>0)- const та такая что , то итерационный процесс, определяемой формулой (3) является сходящимся и предел этой последовательности равен корню узла Геометрическая иллюстрация

Прокомментируем главные условия этой теоремы (4) Пусть 0<φ’<1

Надо найти точки пересечения следующих линий угол от 0 до 45 градусов. Выберем х₀, подставим в правую часть уравнения (2) х₁ в правую часть (2). С увеличением номера приближения х_n все ближе к х*. сходимость на лицо.

Пусть -1<φ’<0 условие (4) выполняется .

С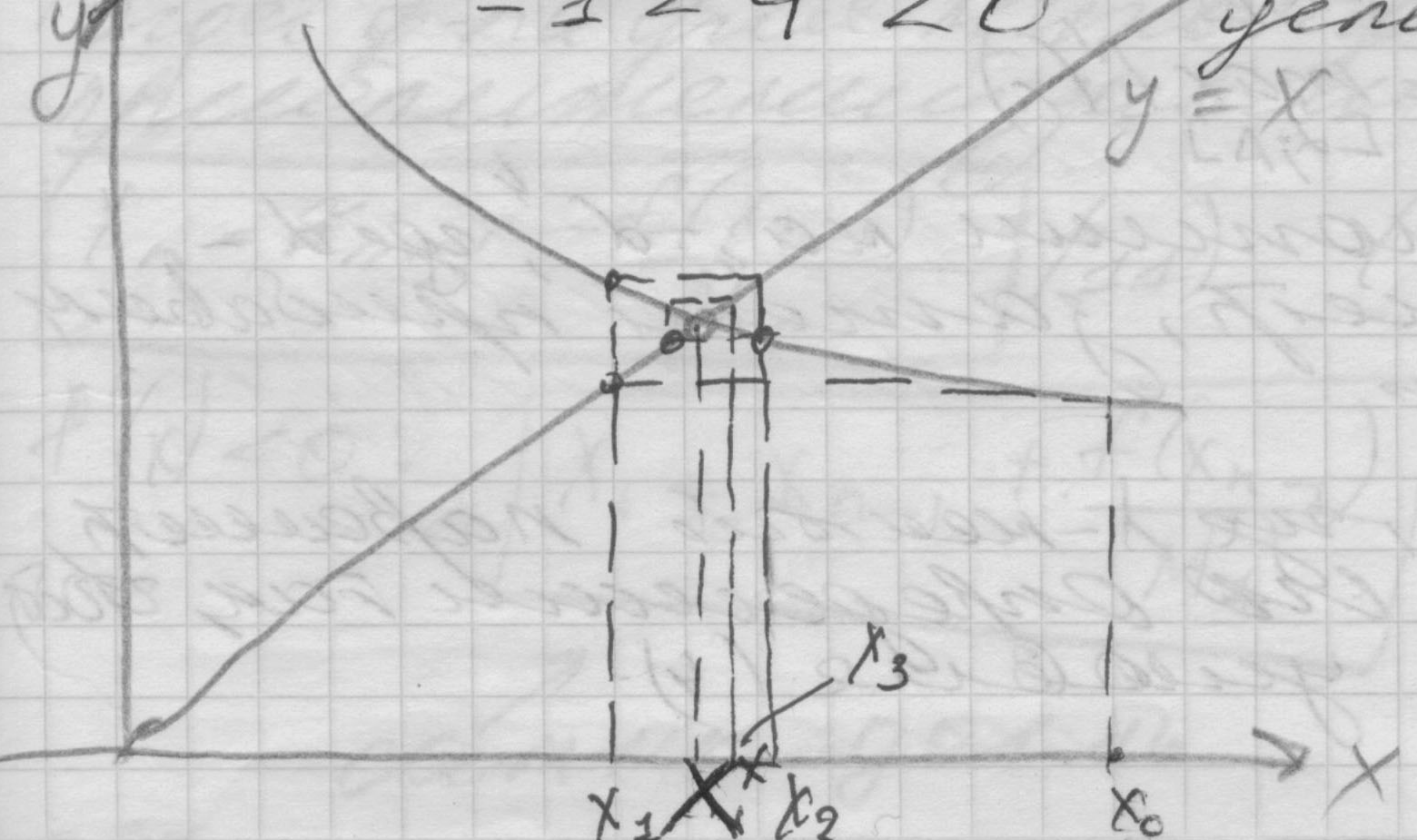 ходящийся

Пусть условие (4) не выполняется φ’>1 С увеличением номера приближения х уходит. Последовательность расходится

Условие (4)- условие сходимости.

Приведение исходного уравнения (1) к виду (2) f(x) =0(1)

И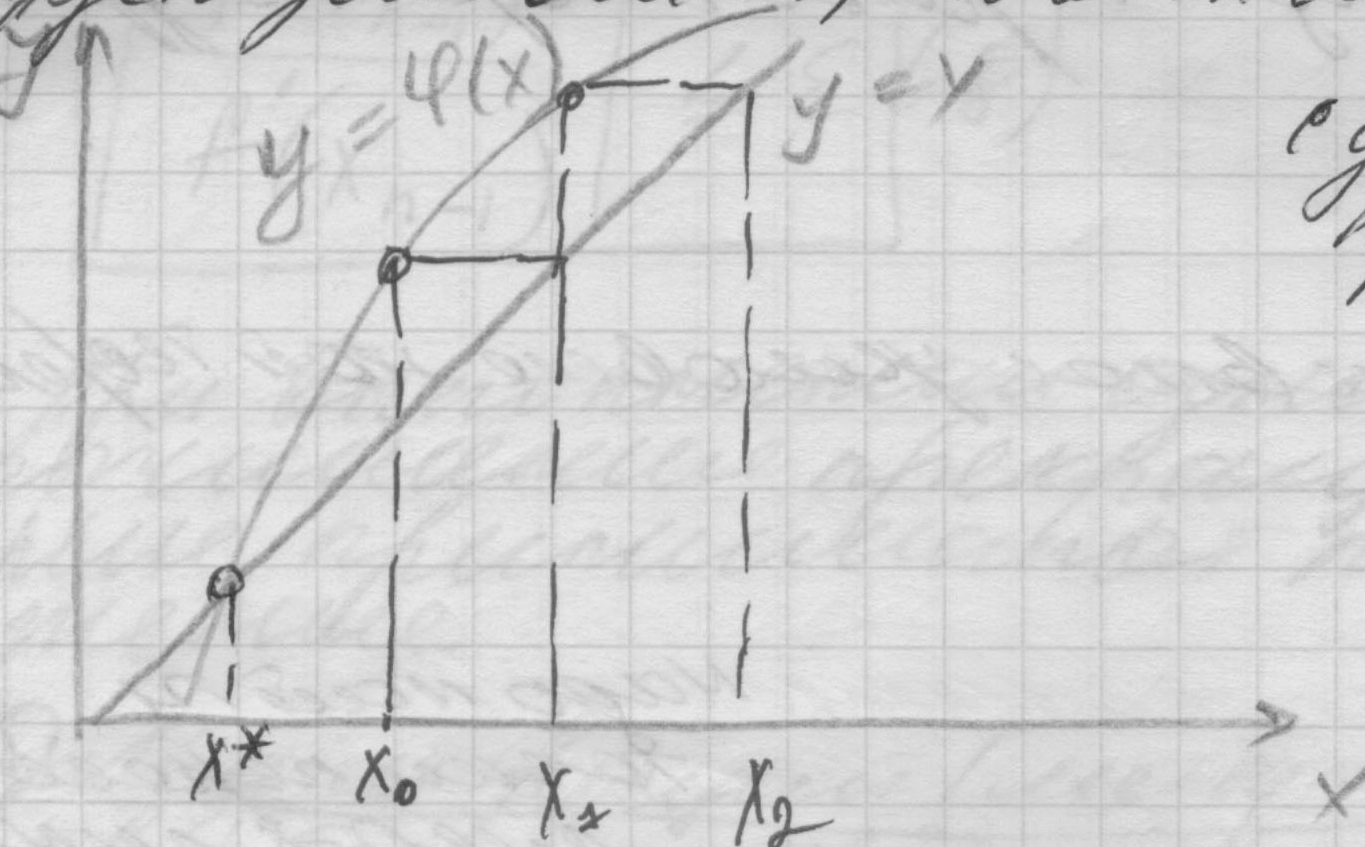 меется достаточно универсальный способ приведения исходного уравнения (1) к виду (2) Пусть для определенности f’(x)>0(случай f’(x)<0- аналогично) обозначим m₁= ;M₁= . Сначала (1) Умножим на «-λ»- где λ- некоторый параметр, затем прибавим по х, получим , где λ-некоторый параметр его определим так чтобы выполнялось условие (4). Найдем . Поставим вместо φ’(x) выражение неравенства (4)

учитывая что >0 | :

, (8). Минимальный диапозон за λ- обычно среднюю точку. . Тогда уравнение (5) Примет вид . Тогда формула для нахождения последовательности х приближений запишется в виде f’(x)<0:

В условии (4) присутствует q. В случае f’(x)>0 за . Вычисления по формуле (3) или (11) продолжаются до выполнения условия . Где q определяется из условия (4). Условие (14) характеризует близость n-го приближения к корню с точностью ε.