Вопрос 1. Численное решение нелинейных уравнений. Два этапа поиска корней уравнения. Графический способ отделения корней уравнения.

f (x)=0 (1)

Где х f(x)-нелинейная функция

Опр1. Уравнения (1) называется алгебраическим, если функция f(x) имеет вид (2) где Другими словами f(x0=P_x(x).

Опр2. Если в функцию входят элементарные функции и ее нельзя преобразовать к виду (2) путем тождественных преобразований, то уравнение (1) называют не трансцендентальным.

Опр3. Корнем уравнения (1) называется точка x* в которой функция тождественно равна 0 f(x*)≡0

1-й этап отделение корней означает изоляцию корней. Это выделение отрезка k- количество корней уравнения содержащих только по одному корню.

Для отделения корней существуют различные способы. В основном используются 2: 1) Графический и 2) Аналитический

2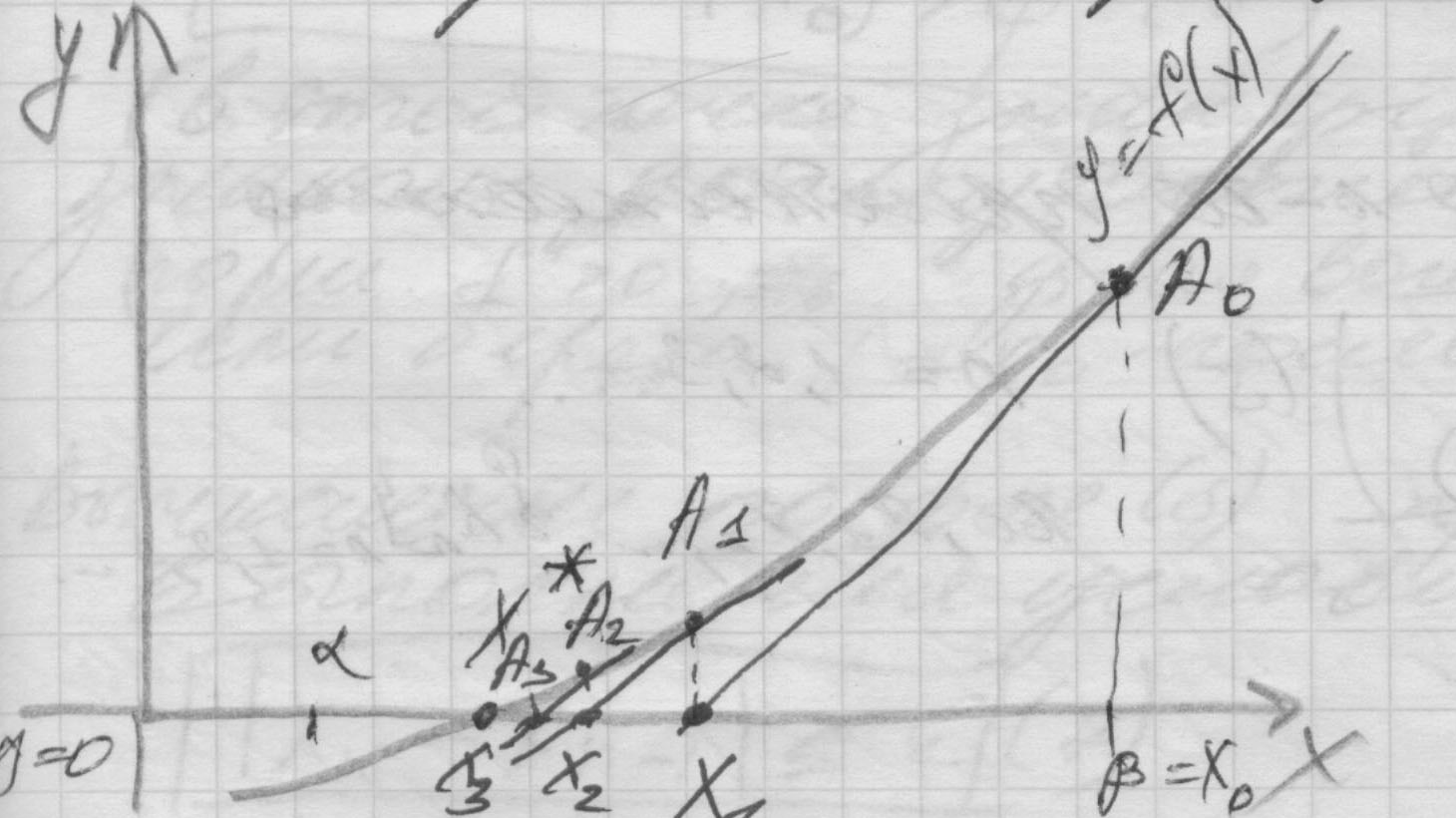 -й тап уточнение корней. На этом этапе к выделенному уравнению на отрезке применяется определенный алгоритм для уточнения корня с заданной степенью точности ε. Другими словами, строится вычислительный процесс, который позволяет определить приближенное значение корня с заданной точностью.

Графический метод

Рассмотрим 2 случая 1) f(x)-простая функция в смысле построения графика 2) f(x)- сложная функция. В первом случае строится график f(x) и за отрезок принимаются участки, содержащие точки пересечения графика с осью ОХ во втором случае f(x) разбивается на 2 более простые функции f₁(x), f₂(x) и уравнение приводиться к виду f₁(x)= f₂(x) затем строят графики функций f₁(x), f₂(x) и за отрезки принимают участки, содержащие абсциссы точек пересечения двух графиков.

Вопрос 2. Аналитический способ отделения корней уравнения.

Для отделения корней можно применить следующую теорему из курса математического анализа.

Теорема Если f(x) непрерывна на отрезке [a,b] и принимает разные значения на его концах, т.е. f(a)*f(b) <0 то на интервале (a,b) имеется по крайней мере одна точка х* такая, что f(x*)=0/

Для того чтобы на (a,b) находился только один корень, в теорему надо ещё добавить условие монотонности f(x) на (a,b) или условие сохранения знака производной на (a,b).

Для отделения корней можно предложить следующий алгоритм :

1)Проверка функций f(x) на непрерывность на отрезке [a,b].

2) нахождение и определение областей монотонности, т.е. решение неравенств >0, <0;

3) выбор таких интервалов монотонности, на концах которых f(x) принимает разные знаки;

4) сужение выбранных в параграфе 3 интервалов.

Из курса математического анализа известно, что любой алгебраический многочлен является непрерывной функцией на всей числовой оси. Поэтому для алгебраических уравнений 1-й пункт алгоритма можно пропустить.

Отрезки , найденные таким образом , будут содержать только по одному корню. Эти отрезки можно рассматривать как начальные приближения корней уравнения(1).

Вопрос 3. Методы уточнения корней нелинейных уравнений. Метод половинного деления.

Метод половинного деления состоит в следующем. Допустим, что корень уравнения (1) отделен и лежит на отрезке . За начальное приближение х₀ примем середину этого отрезка, т.е. . Тогда разделится на два отрезка и Если f(x₀)=0, то х*=х₀. Если , то из двух отрезков и выбираем тот, на концах которого f(x) принимает разные знаки. Обозначим этот отрезок : . Новый отрезок снова делим пополам, при этом ход рассуждений тот же что и в предыдущем случае. Получим отрезок , длинна которого равна . Процесс деления отрезка продолжим до тех пор, пока не получим отрезок такой, что за приближенное значение корня с точностью ε следует взять