2. Цилиндрический шарнир (рис. 2.4) и подшипник (опораВ рис.2.5). Цилиндрическим шарниром называется соединение двух или

более тел посредством цилиндрического стержня, так называемого пальца, вставленного в отверстия в этих телах. Цилиндрический

шарнир препятствует перемеще¬нию по любому направлению в плоскости . Реакция неподвижного цилиндрического

шарнира (шарнирно-неподвижной опоры) представляется в виде неизвестных

составляющих и , линии действия которых параллельны или совпадают с осями координат (рис. 2.4).

3. Подпятник (опора рис. 2.5) и сферический шарнир (рис. 2.6). Такой вид связи можно представить в виде стержня, имеющего на

конце сферическую поверхность, которая крепится в опоре, представляющей собой часть сферической полости. Сферический

шарнир

препятствует перемещению по любому направлению в пространстве, поэтому реакция его представляется в виде трех

составляющих , , , параллельных соответствующим координатным осям.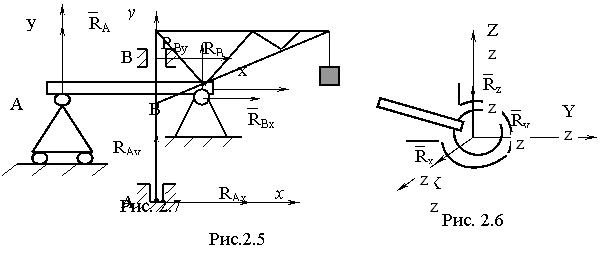

4. Шарнирно-подвижная опора. Этот вид связи конструктивно выполняется в виде цилиндрического шарнира, который может свободно

перемещаться вдоль поверхности. Реакция шарнирно-подвижной опоры всегда направлена перпендикулярно опорной поверхности

(опора рис. 2.7).

5. Шарнирно-неподвижная опора. Реакция шарнирно-неподвижной опоры представляется в виде неизвестных

составляющих и , линии действия которых параллельны или совпадают с осями координат (опора рис. 2.7).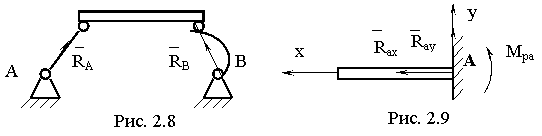

6.Невесомый стержень (прямолинейный или криволинейный), закрепленный по концам шарнирами. Реакция такого стержня является

определенной и направлена вдоль линии, соединяющей центры шарниров (рис. 2.8).

Жесткая заделка. Это необычный вид связи, так как кроме препятствия перемещению в плоскости , жесткая заделка препятствует повороту стержня (балки) относительно точки . Поэтому реакция связи сводится не только к реакции ( , ), но и к реактивному моменту (рис. 2.9).

69 Вопрос

 Статический расчет системы тел сводится к рассмотрению условий равновесия конструкций, состоящих из тел, соединенных какими-нибудь

связями. Связи, соединяющие части конструкции называются внутренними, скрепляющие конструкцию с другими телами, в нее не входящими – 

внешними.

    При решении задач статики реакции связей входят в число неизвестных, которые необходимо определить из уравнений равновесия. Система

тел, для которых число неизвестныхреакций связей равно числу уравнений равновесия, называются статически определимыми. Система тел, для

которых число неизвестных реакций связей больше числа уравненийравновесия, называются статически неопределимыми.

    Если при отбрасывании внешних связей (опор) конструкция остается жесткой, то для нее задача о равновесии решается как для абсолютно

твердого тела (при действии плоской системы сил число неизвестных реакций связей не должно быть больше трех).

    Если после отбрасывания внешних связей конструкция не считается жесткой, то наиболее рациональным способом решения подобных задач

является расчленение на отдельные тела и составление уравнений равновесия для каждого из тел в отдельности.

    Для конструкции из n тел, на каждое из которых действует произвольная плоская система сил, получится таким путем 3n уравнений равновесия,

позволяющих найти 3nнеизвестных.

    Например, если отбросить опоры А и В трехшарнирной арки, то она не будет жесткой: ее части могут поворачиваться вокруг шарнира С.

Для определения реакций внешних связейХ_А, Y_А, Х_В, Y_В   расчленим конструкцию по соединительному шарниру С на две части и рассмотрим

равновесие каждой из частей в отдельности.

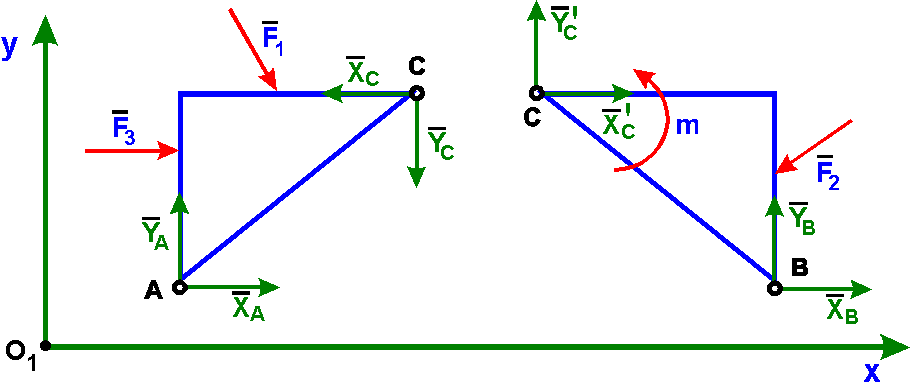
    При действии на трехшарнирную арку произвольной плоской системы сил для каждой части можно записать три уравнений равновесия:

для АС                                            для СВ

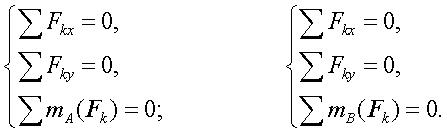
    Присоединить к этой системе шести уравнений на основании закона о действии и противодействии уравнения для узла С (Х_С = Х_Сў, Y_С = Y_Сў), пол

учим систему уравнений из которой можно найти реакции внешних связей Х_А, Y_А, Х_В, Y_В и реакции внутренних связей Х_С, Y_С.