47 вопрос

Скорости тел v₁ и v₂ до удара направлены по их общей нормали, проходящей через их центры масс. Различают две фазы удара:

первая фаза: от момента соприкосновения тел до момента, когда все точки соударяющихся тел приобретут общую скорость u и оба тела получат максимальную деформацию. Скорость u в конце фазы:

где m₁ - масса первого тела; m₂ - масса второго тела;

вторая фаза: с момента окончания первой фазы до того момента, когда тела под действием упругих сил частично восстановят свою форму, приобретут разные скорости u₁ и u₂ и разъединятся. Скорости тел после удара:

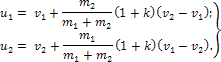
Полный ударный импульс, полученный каждым из тел при ударе:

где знак минус берется для первого тела, а знак плюс для второго.

КИНЕТИЧЕСКАЯ ЭНЕРГИЯ, ПОТЕРЯННАЯ ПРИ УДАРЕ. При ударе часть кинетической энергии ударяющихся тел?T теряется, т. е. переходит в немеханические формы:

где Т* - кинетическая энергия потерянных скоростей v₁-u₁ и v₂-u₂:

Частные случаи: k=0,

k=1, ?T=0 (потери энергии не происходит).

48 вопросТеорема об изменении кинетического момента механической системы при ударе. Изменение кинетического момента механической системы относительно любого неподвижного центра за время удара равно сумме моментов всех внешних ударных импульсов, приложенных к точкам системы, относительно этого же центра.

.

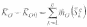Основное уравнение удара для каждой точки системы    ,    .  Так как положение точек системы за время удара не изменяется, то умножая на радиус-вектор  -ой точки   (рис. 18.1), можно записать  ,  .

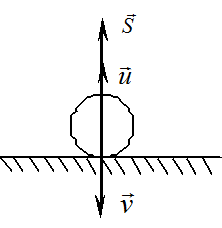
Суммируя полученные равенства,               .

Следствие. Внутренние ударные импульсы не влияют на изменение кинетического момента системы.

49 Вопрос

Предмет и содержание ТМ. Статика, предмет и задачи статики. Основные понятия статики. Аксиомы статики.

Теоретическая механика — одна из древнейших наук, Дайте мне точку опоры и я подниму планету — это оттуда. Сокращенно предмет теоретическая механика называют термех или теормех. В общем это наука об общих законах механического движения и взаимодействия материальных тел. Статика от греч. , неподвижный — раздел механики, в котором изучаются условия равновесия механических систем под действием приложенных к ним сил и моментов. Основные задачи статики. Содержание статики абсолютно твердого тела составляют две основные задачи: 1. Задача о приведении системы сил: как данную систему сил заменить другой, наиболее простой, ей эквивалентной 2. Задача о равновесии: каким условиям должна удовлетворять система сил, приложенная к данному телу или материальной точке, чтобы она была уравновешенной системой Вторая задача часто ставится в тех случаях, когда равновесие заведомо имеет место, например, когда заранее известно, что тело находится в равновесии, которое обеспечивается связями, наложенными на тело. При этом условия равновесия устанавливают зависимость между всеми силами, приложенными к телу. С помощью этих условий удается определить опорные реакции. Нужно иметь в виду, что определение реакций связей внешних и внутренних необходимо для последующего расчета прочности конструкции.

Предмет статики Статика — это раздел механики, в котором излагается общее учение о силах и устанавливаются условия равновесия тел, находящихся под действием сил. Аксиомы статики. Аксиома 1. Если на свободное абсолютно твердое тело действуют две силы, то тело может находиться в равновесии тогда и только тогда, когда эти силы равны по модулю (F1 = F2) и направлены вдоль одной прямой в противоположные стороны .

Аксиома 1 определяет простейшую уравновешенную систему сил, так как опыт показывает, что свободное тело, на которое действует только одна сила, находиться в равновесии не может.

Аксиома 2. Действие данной системы, сил на абсолютно твердое тело не изменится, если к ней прибавить или от нее отнять уравновешенную систему сил.

Эта аксиома устанавливает, что две системы сил, отличающиеся на уравновешенную систему, эквивалентны друг другу.

Следствие из 1-й и 2-й аксиом. Действие силы на абсолютно твердое тело не изменится, если перенести точку приложения силы вдоль ее линии действия в любую другую точку тела.

В самом деле, пусть на твердое тело действует приложенная в точке А сила . Возьмем на линии действия этой силы произвольную точку В и приложим к ней две уравновешенные силы и , такие, что = , = . От этого действие силы на тело не изменится. Но силы и согласно аксиоме 1 также образуют уравновешенную систему, которая может быть отброшена. В результате на тело. Будет действовать только одна сила , равная , но приложенная в точке В.

Таким образом, вектор, изображающий силу , можно считать приложенным в любой точке на линии действия силы (такой вектор называется скользящим).

Аксиома 3 (аксиома параллелограмма сил). Две силы, приложенные к телу в одной точке, имеют равнодействующую, приложенную в той же точке и изображаемую диагональю па­раллелограмма, построенного на этих силах, как на сторонах

Вектор , равный диагонали параллелограмма, построенного на векторах и , называется геометрической суммой векторов и : = + .

Величина равнодействующей

Конечно, Такое равенство будет соблюдаться только при условии, что эти силы направлены по одной прямой в одну сторону. Если же векторы сил окажутся перпендикулярными, то

Следовательно, аксиому 3 можно еще формулировать так: две силы, приложенные к телу в одной точке, имеют равнодействующую, равную геометрической (векторной) сумме этих сил и приложенную в той же точке.

Аксиома 4. При всяком действии одного материального тела на другое имеет место такое же по величине, но противоположное по направлению противодействие.

Закон о равенстве действия и противодействия является одним из основных законов механики. Из него следует, что если тело А действует на тело В с силой , то одновременно тело В действует на тело А с такой же по модулю и направленной вдоль той же прямой, но противоположную сторону силой = . Однако силы и не образуют уравновешенной системы сил, так как они приложены к разным телам.

Аксиома 5 (принцип отвердевания). Равновесие изменяемого (деформируемого) тела, находящегося под действием данной системы сил, не нарушится, если тело считать отвердевшим (абсолютно твердым).

Высказанное в этой аксиоме утверждение очевидно. Например, ясно, что равновесие цепи не нарушится, если ее звенья считать сваренными друг с другом и т. д.