25) Цикл Карно́ и его кпд

Цикл Карно  — идеальный термодинамический цикл. Тепловая машина Карно, работающая по этому циклу, обладает максимальным КПД из всех машин, у которых максимальная и минимальная температуры осуществляемого цикла совпадают соответственно с максимальной и минимальной температурами цикла Карно. Состоит из 2 адиабатических и 2изотермических процессов.

Одним из важных свойств цикла Карно является его обратимость: он может быть проведён как в прямом, так и в обратном направлении, при этом энтропия адиабатически изолированной (без теплообмена с окружающей средой) системы не меняется.

КПД цикла Карно:

Количество теплоты, полученное рабочим телом от нагревателя при изотермическом расширении, равно

.

Аналогично, при изотермическом сжатии рабочее тело отдало холодильнику

.

Отсюда коэффициент полезного действия тепловой машины Карно равен

.

Из последнего выражения видно, что КПД тепловой машины Карно зависит только от температур нагревателя и холодильника. Кроме того, из него следует, что КПД может составлять 100 % только в том случае, если температура холодильника равна абсолютному нулю.

26)Реальные газы. Отличие реальных газов от идеального. Уравнение Ван-Дер-Ваальса.

Реальный газ — газ, который не описывается уравнением состояния идеального газа Клапейрона — Менделеева.

Зависимости между его параметрами показывают, что молекулы в реальном газе взаимодействуют между собой и занимают определенный объём. Состояние реального газа часто на практике описывается обобщённым уравнением Менделеева — Клапейрона:

где p — давление; V - объем T — температура; Z_r = Z_r (p,T)  — коэффициент сжимаемости газа; m - масса; М — молярная масса; R — газовая постоянная.

Отличие реальных газов от идеального:

Молекулы идеального газа не сталкиваются друг с другом, а в реальном газе они движутся сталкиваясь. Идеальный газ поэтому легче рассчитывать. Но в реале идеального газа не существует.

Уравнение Ван-дер-Ваальса — уравнение, связывающее основные термодинамические величины в модели газа Ван-дер-Ваальса.

Для более точного описания поведения реальных газов при низких температурах была создана модель газа Ван-дер-Ваальса, учитывающая силы межмолекулярного взаимодействия. В этой модели внутренняя энергия   становится функцией не только температуры, но и объёма.

Для одного моля газа Ван-дер-Ваальса оно имеет вид:

где

•  — давление,

•  — молярный объём,

•  — абсолютная температура,

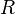•  — универсальная газовая постоянная.

Видно, что это уравнение фактически является уравнением состояния идеального газа с двумя поправками. Поправка   учитывает силы притяжения между молекулами (давление на стенку уменьшается, так как есть силы, втягивающие молекулы приграничного слоя внутрь), поправка   — объем молекул газа.

Для   молей газа Ван-дер-Ваальса уравнение состояния выглядит так:

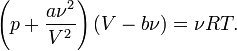
где

•  — объём,

27)Изотермы Ван-Дер-Вальса и их сравнение с эмпирическими изотермами. Критическая точка.

Изотермы Ван-дер-Ваальса — кривые зависимости р от V_m при заданных Т, определяемые уравнением Ван-дер-Ваальс для моля газа. Эти кривые рассматриваются для четырех различных температур; имеют довольно своеобразный характер. При высоких температурах (T > T_к) изотерма реального газа отличается от изотермы идеального газа только некоторым искажением ее формы, оставаясь монотонно спадающей кри­вой. При некоторой температуре T_к на изотерме имеется лишь одна точка перегиба К.

Эта изотерма называется критической, соответствующая ей температура T_к — крити­ческой температурой; точка перегиба К называется критической точкой; в этой точке касательная к ней параллельна оси абсцисс. Соответствующие этой точке объем V_к, и давление р_к называются также критическими. Состояние с критическими парамет­рами (p_к, V_к, T_к) называется критическим состоянием. При низких температурах (Т < T_к ) изотермы имеют волнообразный участок, сначала монотонно опускаясь вниз, затем монотонно поднимаясь вверх и снова монотонно опускаясь.

Проанализируем изотермы уравнения Ван–дер–Ваальса – зависимости Р от V для реального газа при постоянной температуре. Умножив уравнение Ван-дер-Ваальса на V ² и раскрыв скобки, получаем

PV ³ – (RT + bP) vV ² + av²V - abv³ = 0.

Поскольку данное уравнение имеет третью степень относительно V, а коэффициенты при V действительны, то оно имеет либо один, либо три вещественных корня, т.е. изобара Р = const пересекает кривую Р = Р(V) в одной или трех точках, как это изображено на рисунке 7.4. Причем с повышением температуры мы перейдем от немонотонной зависимости Р = Р(V) к монотонной однозначной функции. Изотерма при Т_кр, которая разделяет немонотонные T < T_кр и монотонные T > Т_кр изотермы, соответствует изотерме при критической температуре. При температуре выше критической зависимость Р = Р(V) является однозначной монотонной функцией объема. Это означает, что при T > Т_кр вещество находится только в одном, газообразном состоянии, как это имело место у идеального газа. При температуре газа ниже критической такая однозначность исчезает, а это означает возможность перехода вещества из газообразного в жидкое и наоборот. На участке АСВ изотермы Т₁ давление растет с увеличением объема (dP/dV) > 0. Данное состояние неустойчиво, поскольку здесь должны усиливаться малейшие флуктуации плотности. Поэтому область ВСА не может устойчиво существовать. В областях DLB и AGE давление падает с увеличением объема (dP/dV)_Т < 0 – это необходимое, но не достаточное условие устойчивого равновесия. Эксперимент показывает, что система переходит из области устойчивых состояний GE (газ) в область устойчивых состояний LD(жидкость) через двухфазное состояние (газ – жидкость) GL вдоль горизонтальной изотермы GCL.

При квазистатическом сжатии, начиная с точки G, система распадается на 2 фазы – жидкость и газ, причем плотности жидкости и газа остаются при сжатии неизменными и равными их значениям в точках L и G соответственно. При сжатии количество вещества в газообразной фазе непрерывно уменьшается, а в жидкой фазе – увеличивается, пока не будет достигнута точка L, в которой все вещество перейдет в жидкое состояние.

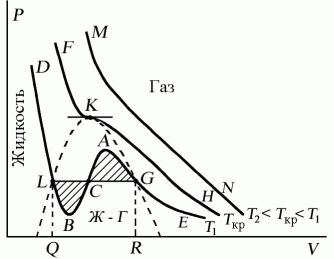  Рис. 7.4

Наличие критической точки на изотерме Ван–дер–Ваальса означает, что для каждой жидкости существует такая температура, выше которой вещество может существовать только в газообразном состоянии

Критическую точку K мы определили как точку перегиба критической изотермы, в которой касательная к изотерме горизонтальна (рис. 7.5). Ее можно определить также как точку, в которую в пределе переходят горизонтальные участки изотерм при повышении температуры до критической. На этом основан способ определения критических параметров P_k, V_k, Т_k, принадлежащий Эндрюсу. Строится система изотерм при различных температурах. Предельная изотерма, у которой горизонтальный участок LG (рис. 7.4) переходит в точку, будет критической изотермой, а указанная точка – критической точкой 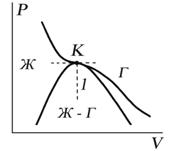(рис. 7.5).

  Рис. 7.5

Недостаток способа Эндрюса заключается в его громоздкости.