14)Первое начало термодинамики. Его физический смысл.

Первое начало термодинамики — один из трёх основных законов термодинамики, представляет собой закон сохранения энергии длятермодинамических систем.

Существует несколько эквивалентных формулировок первого начала термодинамики

В любой изолированной системе запас энергии остаётся постоянным.^[2] Это — формулировка Дж. П. Джоуля (1842 г.).

Количество теплоты, полученное системой, идёт на изменение её внутренней энергии и совершение работы против внешних сил

Изменение внутренней энергии системы при переходе её из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе, то есть, оно зависит только от начального и конечного состояния системы и не зависит от способа, которым осуществляется этот переход. Это определение особенно важно для химической термодинамики^[2] (ввиду сложности рассматриваемых процессов). Иными словами, внутренняя энергия является функцией состояния. В циклическом процессе внутренняя энергия не изменяется.

Изменение полной энергии системы в квазистатическом процессе равно количеству теплоты  , сообщённому системе, в сумме с изменением энергии, связанной с количеством вещества   при химическом потенциале  , и работы  ^[3], совершённой над системой внешними силами и полями, за вычетом работы  , совершённой самой системой против внешних сил

.

Для элементарного количества теплоты  , элементарной работы   и малого приращения   внутренней энергии первый закон термодинамики имеет вид:

.

Разделение работы на две части, одна из которых описывает работу, совершённую над системой, а вторая — работу, совершённую самой системой, подчёркивает, что эти работы могут быть совершены силами разной природы вследствие разных источников сил.

Важно заметить, что   и   являются полными дифференциалами, а   и   — нет.

15)Применение первого начала термодинамики к изопроцессам.

Среди равновесных процессов, которые происходят с термодинамическими системами, отдельно рассматриваются изопроцессы, при которых один из основных параметров состояния остается постоянным.  Изохорный процесс (V=const). Диаграмма этого процесса (изохора) в координатах р, V изображается прямой, параллельной оси ординат (рис. 1), где процесс 1—2 есть изохорное нагревание, а 1—3 — изохорное охлаждение. При изохорном процессе газ не совершает работы над внешними телами, т. е.    Из первого начала термодинамики (δQ=dU+δA) для изохорного процесса следует, что вся теплота, которая сообщается газу, идет на увеличение его внутренней энергии:    т.к. C_V=dU_m/dt,    Тогда для произвольной массы газа получим   (1)  Изобарный процесс (p=const). Диаграмма этого процесса (изобара) в координатах р, V изображается прямой, которая параллельна оси V. При изобарном процессе работа газа при увеличения объема от V₁ до V₂ равна   (2)  и равна площади заштрихованного прямоугольника (рис. 2). Если использовать уравнение Менделеева-Клапейрона для выбранных нами двух состояний, то   и    откуда    Тогда выражение (2) для работы изобарного расширения примет вид   (3)  Из этого выражения вытекает физический смысл молярной газовой постоянной R: если T₂ —T₁ = 1К, то для 1 моль газа R=A, т. е. R численно равна работе изобарного расширения 1 моль идеального газа при нагревании его на 1 К. 

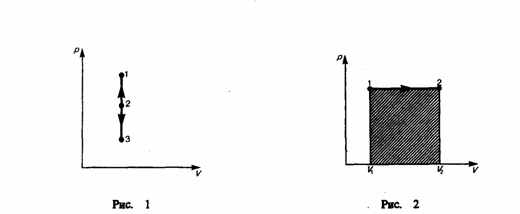
Рис.1

В изобарном процессе при сообщении газу массой m количества теплоты    его внутренняя энергия возрастает на величину (т.к. C_V=dU_m/dt)    При этом газ совершит работу, определяемую выражением (3).  Изотермический процесс (T=const). Изотермический процесс описывается законом Бойля—Мариотта:    Диаграмма этого процесса (изотерма) в координатах р, V представляет собой гиперболу, которая расположена на диаграмме тем выше, чем выше температура, при которой происходит процесс.  Исходя из формул для работы газа и уравнения Менделеева-Клайперона найдем работу изотермического расширения газа:    Так как при Т=const внутренняя энергия идеального газа не изменяется:    то из первого начала термодинамики (δQ=dU+δA) следует, что для изотермического процесса    т. е. все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил:   (4)  Значит, для того чтобы при расширении газа температура не становилась меньше, к газу в течение изотермического процесса необходимо подводить количество теплоты, равное внешней работе расширения.