1. Математическое ожидание (expected value) случайной величины

В обычной жизни известно, как среднее арифметическое.   

2.Дисперсия (variance) случайной величины.

    

3. Cтандартное отклонение (standard deviation). Одно из важнейших понятий математической статистики.

Другое название - среднеквадратичное отклонение.     

4. коэффициент асимметрии:

.

5. Эксцесс

.

28. Спектрально-коррелляционные характеристики классификации текстур.

Помимо статистических характеристик необходимо оценивать параметры, которые были бы присущи самой форме текстуры. Как правило, в качестве таких характеристик используется или энергетический спектр текстуры или автокорреляционная функция.

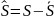- автоковариационная функция.

S – изображение, автокорреляционная функция.

Для автоматизации процедуры определения порога и установления адаптивного уровня порога применяется гистограмма относительных частот появления определенных уровней в энергетическом спектре изображения.

Относительная частота интенсивности g-го пикселя определяется:

Pf=ng/(MN)

где g = 0,1,…,G-1 – значение интенсивности пикселя;

ng – количество элементов изображения с уровнем g;

M – количество строк изображения;

N – количество столбцов изображения.

После расчета гистограммы происходит вычисление локальных минимумов с использованием преобразования Гильберта:

Порог для последующей бинаризации изображения энергетического спектра выбирается автоматически из локальных минимумов гистограммы. Предлагается использовать для распознавания и классификации текстур систему признаков, которая формируется при расчете геометрических моментов признаков бинаризованного энергетического спектра изображения и признаков формы. Как классификационные признаки геометрические моменты в полярной системе координат обладают рядом достоинств. Признаки инвариантны к масштабу, что позволяет производить классификацию при различных размерах обрабатываемого фрагмента и исходного изображения. Интегрирование по углу обеспечивает инвариантность к повороту фигуры. Признаки инвариантны к параллельному переносу, поскольку полюс системы координат совмещается с центром тяжести фигуры. Число признаков легко наращивается без перестройки алгоритма вычисления до достижения устойчивого распознавания. Для распознавания и классификации текстурной области по форме энергетического спектра достаточно иметь информацию о его контуре. Имея полную информацию о контуре, легко определить площадь, координаты центра тяжести и морфометрические признаки, а также геометрические моменты признаков.

30. Выделение информативных признаков сигналов и изображений в пространстве параметров модели линейного предсказания.

Выделение информативных признаков для решения задачи распознавания сигналов и изображений представляется как задача многокритериальной оптимизации.

Пусть Ω – множество различных подмножеств признаков, характеризующих объект данных. Каждое подмножество представляет собой некоторую комбинацию входных признаков из максимально возможного количества комбинаций 2ⁿ, где n – количество входных признаков. Требуется выделить подмножество признаков S є Ω , которое является решением двухкритериальной задачи оптимизации с двумя следующими критериям:

max f1(S), min f2(S), (1)

где f1(S) – количество правильно классифицированных объектов с использованием подмножества признаков S, f2(S) – количество элементов подмножества признаков S.

В предлагаемом подходе для выделения признаков использован генетический алгоритм, который имеет модифицированную схему реализации применительно к задаче многокритериальной оптимизации. Согласно алгоритму не требуется изначальное определение весовых коэффициентов, соответствующих отдельным целевым критериям [3]. Решение задачи оптимизации в этом случае можно получить в виде нескольких недоминируемых подмножеств признаков.

Для расчета точности классификации с использованием подмножества признаков используется алгоритм k-ближайших соседей [4]. Согласно этому алгоритму для каждого объекта определяется k-ближайших соседей в пространстве признаков. Выбор соседей обычно выполняется на основании значений евклидовых расстояний, хотя можно использовать другие метрики (например, расстояние Махаланобиса). В качестве класса объекта выбирается класс, к которому относятся большинство из k-ближайших соседей.

Лине́йное предсказа́ние (англ. linear prediction) — вычислительная процедура, позволяющая по некоторому набору предшествующих отсчётов цифрового сигнала предсказать текущий отсчёт.

Пусть s(i) — анализируемый цифровой сигнал. При линейном предсказании оценка текущего отсчёта сигнала формируется как линейная комбинация предшествующих отсчётов:

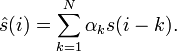
Задача линейного предсказания заключается в том, чтобы найти набор коэффициентов {α_k}, при котором средний квадрат ошибки предсказания минимален:

.

Величина N называется порядком линейного предсказания.