17. Рекуррентные сети (ассоциативная память).

Отдельную группу нейронных сетей составляют сети с обратной связью между различными слоями нейронов. Это так называемые рекуррентные сети. Их общая черта состоит в передаче сигналов с выходного либо скрытого слоя на входной слой.

Благодаря обратной связи при подаче сигнала на входы сети, в ней возникает переходный процесс, который завершается формированием нового устойчивого состояния, отличающегося в общем случае от предыдущего. Если функцию активации нейрона обозначить f(u), где u - взвешенная сумма его возбуждений, то состояние нейрона можно определить выходным сигналом y=f(u)=f(u₁x₁+…+u_Nx_N⁾. Изменение состояния i-го нейрона можно описать системой дифференциальных уравнений .

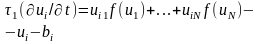для i=1,2,…,N, где b_i - пороговое значение.

Рекуррентной сети можно поставить в соответствие энергетическую функцию Ляпунова

Изменение состояния какого-либо нейрона инициализирует изменение энергетического состояния сети в направлении минимума ее энергии вплоть до его достижения. В пространстве состояний локальные энергетические минимумы E представлены точками стабильности, называемыми аттракторами из-за тяготения к ним ближайшего окружения. Благодаря наличию аттракторов, рекуррентные сети могут быть использованы как устройства ассоциативной памяти.

Ассоциативная память играет роль системы, определяющей взаимную зависимость векторов. В случае, когда на взаимозависимость исследуются компоненты одного и того же вектора, говорят об автоассоциативной памяти. Если же взаимозависимыми оказываются два различных вектора, можно говорить о памяти гетероассоциативного типа. К первому классу относится сеть Хопфилда, а ко второму - сеть Хемминга и сеть типа BAM (Bidirectional Associative Memory - двунаправленная ассоциативная память).

Задача ассоциативной памяти сводится к запоминанию обучающих векторов, чтобы при представлении нового вектора система могла сгенерировать ответ - какой из запомненных ранее векторов наиболее близок к вновь поступившему образу. Часто в качестве меры близости отдельных множеств применяется расстояние Хемминга.

При использовании двоичных значений (0,1) расстояние Хемминга между двумя векторами y=(y₁,y₂,y_n) и d=(d₁,d₂,d_n) определяется в виде

При биполярных значениях элементов обоих векторов расстояние Хемминга рассчитывается по формуле

Мера Хемминга равна числу несовпадающих компонент двух векторов.

18. Сеть Хопфилда как ассоциативная память

Структурная схема сети Хопфилда состоит из единственного слоя нейронов, число которых является одновременно числом входов и выходов сети. Каждый нейрон связан синапсами со всеми остальными нейронами, а также имеет один входной синапс, через который осуществляется ввод сигнала. Выходные сигналы, как обычно, образуются на аксонах.

Задача, решаемая данной сетью в качестве ассоциативной памяти, как правило, формулируется следующим образом. Известен некоторый набор двоичных сигналов (изображений, звуковых оцифровок, прочих данных, описывающих некие объекты или характеристики процессов), которые считаются образцовыми. Сеть должна уметь из произвольного неидеального сигнала, поданного на ее вход, выделить («вспомнить» по частичной информации) соответствующий образец (если такой есть) или «дать заключение» о том, что входные данные не соответствуют ни одному из образцов. В общем случае любой сигнал может быть описан вектором ,n — число нейронов в сети и размерность входных и выходных векторов. Каждый элемент , равен либо +1, либо -1. Обозначим вектор, описывающий k-й образец, через , а его компоненты, соответственно, как , где m – в данном случае число образцов. Когда сеть распознает (или «вспомнит») какой-либо образец на основе предъявленных ей данных, ее выходы будут содержать именно его, то есть Y = Xk, где Y — вектор выходных значений сети: Y = {yi: i = 1, 2, ..., n}. В противном случае выходной вектор не совпадет ни с одним образцовым.

Если, например, сигналы представляют собой некие изображения, то, отобразив в графическом виде данные с выхода сети, можно будет увидеть картинку, полностью совпадающую с одной из образцовых (в случае успеха) или же «вольную импровизацию» сети (в случае неудачи).

На стадии инициализации сети весовые коэффициенты синапсов устанавливаются следующим образом:

Здесь i и j — индексы, соответственно, предсинаптического и постсинаптического нейронов; , – i-й и j-й элементы вектора k-гo образца.

Алгоритм функционирования сети следующий (t — номер итерации):

1.На входы сети подается неизвестный сигнал. Фактически его ввод осуществляется непосредственной установкой значений аксонов: yi (0)=xi, i=1, 2,….n, поэтому обозначение на схеме сети входных синапсов в явном виде носит чисто условный характер. Ноль в скобке справа от у, означает нулевую итерацию в цикле работы сети.

2.Рассчитываются новое состояние нейронов и новое значение аксонов где f – пороговая активационная функция.

3.Проверка, изменились ли выходные значения аксонов за последнюю итерацию. Если да — переход к п.2, иначе (если выходы стабилизировались) - конец работы. При этом, выходной вектор представляет собой образен, наилучшим образом сочетающийся с входными данными.

Таким образом, когда подается новый вектор, сеть переходит из вершины в вершину, пока не стабилизируется. Устойчивая вершина определяется сетевыми весами и текущими входами. Если входной вектор частично неправилен или неполон, сеть стабилизируется в вершине, ближайшей к желаемой.

Показано, что достаточным условием устойчивой работы такой сети является выполнение условии

Как говорилось выше, иногда сеть не может провести распознавание и выдает на выходе несуществующий образ. Это связано с проблемой ограниченности возможностей сети. Для сети Хопфилда число запоминаемых образов N не должно превышать величины, примерно равной . Кроме того, если два образа А и В очень похожи, они, возможно, будут вызывать у сети перекрестные ассоциации, то есть предъявление на входы сети вектора А приведет к появлению на се выходах вектора В и наоборот.