26. Векторне, канонічні і параметричні рівняння прямої у просторі. Кут між прямими в просторі. Кут між прямою й площиною. Умови паралельності й перпендикулярності прямих, прямій і площині

Виберемо на прямій довільну точку М(x, y, z) і запишемо умову колінеарності векторів

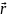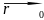= − = і : − =t , −∞<t<+∞,

де t − скалярний множник (параметр). Рівняння називається векторним рівнянням прямої у просторі.

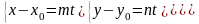- параметричне рівн прямої -канонічні рівняння прямої

cos = = 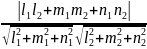-Косинус гострого кута між прямими

Синус гострого кута між прямою й площиною дорівнює косинусукута θ між напрямним вектором прямої і вектором нормалі до площини sin =cos = =

Умова паралельності прямої і площини:

Al + Bm+ Cn = 0.

Умови перпендикулярності прямої і площини:

.

27.Рівняння прямої у r3, що проходить через дві дані точки. Рівняння прямої як лінії перетину двох площин. Перехід до канонічних рівнянь прямої

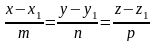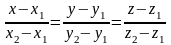Визначимо розташування прямої у просторі двома точками .Запишемо канонічне рівн.прямої, що проход, через т. М1, скориставшись рівнянням. Потребуємо щоб дана пряма проходила через т.М₂ тобто координати т.М₂ повинні задовольняти дане рівняння. . Замість (м;п;р)підставимо величини (х₂-х₁;у₂-у₁;z₂-z₁) їм пропорційні. Одержимо: рівняння прямої, що проходить через 2 дані точки.

Рівняння прямої у просторі можна розглядати як перетин двох непаралельних площин система визначає загальне рівн.прямої у просторі, якщо коефіц A₁,B_1,C_1,- непропорційні A₂,B₂,C_2. Від загального рівн.прямої можна перейти до канонічного рівн. Для цього потрібно розв’язати систему. Виберемо базисний мінор відмінний від 0, а одну із змінних об'явимо рівною. Одержомо систему. А_1,В₁ А_2,В₂-базисний мінор Дану систему розв’яжемо за формулою Крамера таким чином ми одержимо значення х і у виражено через z. Далі виключимо З цих рівнянь і знайдемо шукане рівняння.

Необхідно скласти рівняння площини, що проходить через дану пряму. 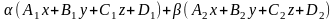рівняння площини, що проходить через дану пряму.1)Можливе наступне, якщо

2)Якщо , то одержимо

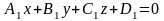
3) Якщо , то тоді одержимо … рівняння визначає рівняння площини, що проходить через дану пряму, де і -довільні числа.

Так як і -довільні числа.

, то через дану пряму можна провести нескінченну множину площин, а тому рівняння називається рівнянням жмутка площин, що проходить через дану пряму.

28. Функція однієї змінної, означення. Способи завдання функцій. Основні елементарні функції і їх графіки

Фу́нкція— це правило, яке кожному елементу з першої множини ставить у відповідність один і тільки один елемент з другої множини.

Функція може бути задана аналітично, графічно, таблицею й алгоритмом.

1. Аналітичний спосіб. Функція задається формулою (формулами) аборівнянням, що зв’язує аргумент x та залежну змінну y. Під областювизначення мають на увазі сукупність значень аргументу, для яких

аналітичний вираз має зміст і набуває дійсних значень (ОДЗ).

Наприклад,

1) y = + 2;

2) y=

3) 2x − 3y + 1 = 0.

2. Графічний спосіб. Задається графік функції, тобто множина точокплощини з координатами (х, f(x)).

3. Табличний спосіб. Задається таблиця певних значень аргументу тавідповідних їм значень функції.

4. Алгоритмічний спосіб. Задається алгоритм − сукупність арифметичних і логічних операцій, які потрібно здійснити над аргументом, щоб одержати значення функції.