16.Пряма на площині. Рівняння прямої: векторне, загальне, із кутовим коефіцієнтом, у відрізках, що проходить через дві дані точки.

R-R₀= St- векторне рівняння прямої

А_х + В_х + С = 0. -загальне рівняння прямої

У= kx+b—це рівняння прямої з кутовим коефіцієнтом

х/а+у/в=1- рівняння прямої у відрізках на осях

y-y₀= k(x-x₀)- рівняння жмутка прямих, що проходять через дану точку.

17. Нормальне рівняння прямої на площині. Зведення загального рівняння прямої до нормального вигляду. Відстань від точки до прямої.

x cosα+y sinα−p=0- нормальне рівняння прямої

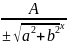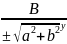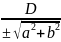+ + -0-Зведення загального рівняння прямої донормального вигляду

Відстань від точки K(x1, y1) до прямої дорівнює модулю відхилення й обчислюється за такими формулами:

• пряма задана нормальним рівнянням

d = x1 cosα+y1 sinα−p

Відстань від точки до прямої.

18.Кут між двома прямими. Умови паралельності й перпендикулярності прямих

Кутом між двома прямими називається кут між його нормальними векторами.

(l1) N1 (A1 B1)

(l2) N2 ( A2 B2) Cos γ N1 N2 / | N1| × | N2|

Cos γ = A1 A2 + B1 B2 / sqr( A12 + B12 ) × sqr( A22 + B22)

Умова паралельності:

L1 || L2  N1 || N2 A1 / A2 = B1 / B2

Умова перпендикулярності:

L1 перпенд. L2  N1 перпенд. N2 A1 A2 + B1 B2 = 0

Якщо прямі задані з кутовим коефіцієнтом:

{ y = k1x + b1

{ y = k2x + b2

Tq γ = k2 – k1 / 1 + k1k2

19. Еліпс. Канонічне рівняння еліпса. Ексцентриситет, фокуси. Основна властивість

Еліпсом називається множина точок площини, сума відстаней яких до двох фіксованих точок, що називаються фокусами, є величина ста­ла 2а і більше ніж відстань між фокусами (2а> 2с).

Нехай задано 2 точки F₁ і F₂ : | F₁ F₂|=2c, проведемо прямокутну сист. коорд. так, щоб точки F₁ F₂ лежали на осы ОХ, а початок координат ділили відрізок F₁ F₂ навпіл, тоді т. F₁ (-c ; 0); F (c;0).

x²/ a² + y²/b² =1 канонічне рівняння еліпса

малюнок |A₁ O| = |O A₂ | = a велика піввісь еліпса.

|B₁ O | = |O B₂ | = b мала піввісь еліпса.

A₁A₁ = 2a велика вісь.

B₁ B₂ = 2b мала вісь.

F₁ (-c; 0) ,F₂ (0; c) фокуси еліпса.

Ексцентриситетом еліпса наз. величина, що довіює відношенню відстані між фокусами до довжини великої осі .

Ε=2c/2a=c/a>1 c =|OF₁| = |OF₂| фокусна відстань

Чим більше ексцентрис. Тим більше еліпс витягнутий вздовж длинної осі, чим менше тим більше похоже на коло.

20.Гіпербола. Канонічне рівняння, ексцентриситет, фокуси, асимптоти. Основна властивість гіперболи

Гіперболою наз. множина точок площини, модуль різниці відстаней від кожної із яких до двох даних точок, що наз. фокусами є величина стала 2а і менша, ніж відстань від фокусами.

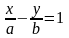,де b²=c²-a² називається канонічним рівнянням.

Дослідимо форму гіперболи: рівняння містить змінні х та у в парних степенях. Це означає, що разом з точкою (х, у ), яка належить гіперболі, їй належать і точки (-х, у), (-х, -у), ( х, -у ),тому гіпербола симетрична відносно осей ОХ, ОУ та відносно точки О (0,0), яка називається центром гіперболи. Розв`яжемо рівняння відносно у: маємо

При | х | < а значення існує, тому для гіперболи |х | 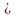а.

Гіпербола перетинає вісь ОХ у двох точках А₁(а, 0) і А₂( -а ,0). Гіпербола вісь ОУ не перетинає. Точки А₁ і А₂ – називаються вершинами гіперболи. Відрізок А₁А₂=2а називається довжиною дійсної осі гіперболи.

Точки В₁(0, b) і B₂(0? –b) називаються уявними вершинами гіперболи.

Асимптотою гіперболи наз. пряма з властивістю точок, які віддаляються по криві у нескінченність, необмежено наближаючись до цієї прямої.

Прямі 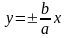є асимптотою гіперболи. Асимптоти гіперболи характеризують її форму. Гіпербола з рівними півосями (a = b ) наз. рівносторонньою, а її канонічне рівняння має вигляд x²-y² =a².

Прямокутником рівносторонньої гіперболи є квадрат із стороною 2а, а її асимптоти –бісектриси координатних кутів.

До фокальних властивостей гіперболи належать поняття ексцентриситету та директрис.

Ексцентриситетом гіперболи наз. відношення відстаней між її фокусами до довжини її дійної осі гіперболи знаходяться на відстані 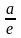від початку координат.

Відношення довжини фокальних радіусів кожної точки гіперболи до відстаней цієї самої точки від відповідних директрис є величина стала і дорівнює ексцентриситету гіперболи, тобто .
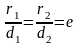