12.Лінійний векторний простір.Лінійно-залежні і лінійно-незалежні системи векторів. Базис простору. Розкладання вектора за базисом.N-вимірний вектор
Сукупність
векторів у просторі, після введення в
неї операцій додавання і множення на
число називається трьохвимірним
векторним простором і позначається a.
Аналізуя сукупність векторів на площині
, назвемо лінійним векторним простором
.
На прямій – одновимірним лінійним
простором
.
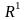Простір
,
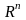завжди містить нульовий вектор. Простір
,
завжди замкнутий відносно операцій
додавання і множення вектора на число.
Лінійною комбінацією векторів
називається вираз виду
,
де
-
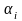деякі числа. Тобто під лінійною
комбінацією векторів розуміюь новий
вектор, який одержуємо в результаті
лінійних операцій над векторами. Система
векторів
називається лінійно
незалежною,
якщо рівність
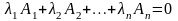
виконується лише за умови
.
Якщо
рівність (2.1) можлива хоча б при одному
із чисел
,
то система векторів називається лінійно
залежною.
Можна сформулювати еквівалентне означення:
система векторів називається лінійно залежною, якщо хоча б один із векторів системи є лінійною комбінацією решти векторів системи. Наприклад:
.
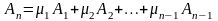Якщо якась підсистема системи векторів лінійно залежна, то і вся система лінійно залежна. Якщо система векторів лінійно незалежна, то і довільна її підсистема теж лінійно незалежна.
Розглянемо
лінійно залежну систему векторів
Візьмемо таку лінійно незалежну
підсистему
,
до якої не можна додати жодного вектора,
щоб не порушити лінійну незалежність.
Таку систему називають максимальною
лінійно незалежною підсистемою
даної системи векторів.
Кількість векторів, які входять в довільну максимально лінійно незалежну підсистему векторів, називають рангом системи векторів.
Розглянемо систему векторів
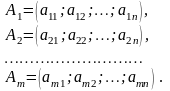
Ранг системи векторів дорівнює рангу матриці, яка утворена координатами векторів цієї системи, тобто рангу матриці
.
Таким
чином, якщо система векторів
лінійно-залежна, то один з цих векторів
можна представити у вигляді лінійної
комбінації решти векторів. Нехай лінійна
комбінація векторів=0. Припустимо, що
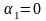
Числа
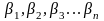називаються коефіцієнтами розкладу,
найчастіше використовується розклад
за базисом. Базисом n-вимірного
простору називається сукупність
n-лінійно-незалежних
векторів цього простору. Базисом на
прямій є любий ненульовий вектор, що
лежить на цій прямій. Базисом на площині
наз. два любих неколініарних вектори.
Базисом у просторі називаються три
компланарні вектори. Нульовий простір
базису не має, так як не містить
лінійно-незалежних векторів. Нескінченно
- вимірний простір, в якому число базисних
векторів невизначено, також не має
базису. Мають місце наступні твердження:
1) Любі два неколініарні вектори утворюють базис
2) Трикомпланарні вектори завжди лінійно-залежні. Упорядкована система дійсних чисел
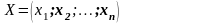
називається -вимірним вектором.
Числа
називаються координатами
вектора.