64.Визначений інтеграл, як границя інтегральної суми. Теорема існування. Геометричний зміст визначеного інтеграла.

Скінченна границя інтегральної суми, при умові, що число відрізків n прямує до нескінченності, а довжина найбільшого з них прямує до 0 наз. Визначеним інтегралом функції y = f(x) в межах х = а, х = в і позначається

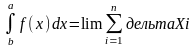
Теорема існування визначеного інтегралу.

Якщо функція y = f(x) визначена на відрізку [a,b] або має на цьому відрізку лише точки скінченого розриву, то визначений інтеграл існує для цієї функції і він єдиний.

Геометричний зміст визначеного інтегралу.

Нехай дано функцію y = f(x),яка визначена на відрізку [a,b], причому f(x)>=0. Потрібно знайти S криволінійної трапеції аАВв, обмеженою лініями х = а, х = в, у = 0, у= f(x)/

Малюнок

1). Розіб’ємо відрізок АВ на n частин точками Хі, і=0, а = Х0<X1<X2<Xn= в.

2). Позначимо через дельта Х = Хі+1 –Хі .

3). В кожному з відрізків [ Xi-1 +Xi], виберемо довільну точку Ei [ Xi-1, Xi] і обчислемо

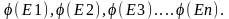
4). В кожному частинному проміжку побудуємо прямокутник, висота якого є 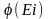, а основа (дельта) Хі.

_{5). Визначимо суму}

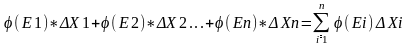
65.Властивості визначеного інтеграла.

1. Сталий множник можна винести за знак інтеграла.

2.Визначений інтеграл від алгебраїчної суми скінченого числа неперервних функцій дорівнює сумі їх інтегралів.

3.Визначений інтеграл з однаковими межами інтегрування = 0.

4.Якщо у визначеному інтегралі поміняти місцями межі інтегрування , то знак перед інтегралом зміниться на протилежний.

5. Для любих чисел а ,в ,с справедлива рівність: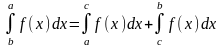

6. Якщо функція f(x) і g(x) неперервні на відрізку [ a ,b] , f(x)>=g(x), то

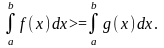
7.Якщо m і M найменше і найбільше значення функції на відрізку [a, b], то 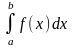знаходиться в межах: m(b-a) <= <= M(b-a).

8. Якщо функція y = f(x) на [a,b] неперервна, то існує така точка С є[a,b], що f( c) = .

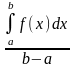66.Визначений інтеграл із змінною, верхньою межею і його похідна на поверхній межі. Нехай y=f(x) неперервна на відрізку [a,b] , тоді визначений інтеграл існує і дорівнює деякому числу. Якщо в інтегралі нижню межу «а» зафіксувати, а «б» - замінити змінною х, де х є [a,b], то одержимо: (2). Змінною інтегрування ми позначимо буквою t, щоб відрізнити її від змінної верхньої межі. Інтеграл (2) буде залежать від положення т.Х, тобто інтеграл(2) є деяка функція своєї верхньої межі.

Теорема:

Нехай функція f(t) неперервна скрізь на проміжку [a,x], тоді похідна від визначеного інтегралу по змінній верхній межі х дорівнює підінтегральній функції в якій змінна інтегрування замінена цією межею.

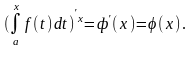
67. Формула Ньютона-Лейбніца.

Якщо функція f(x) є неперервною на [a,b], a F(x) є однією з її первісних на [a,b], то має місце формула:

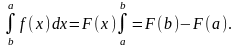
68. Заміна змінної у визначеному інтегралі.

Нехай дано інтеграл 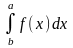, де f(x) неперервна на відрізку [a,b]. Введемо нову змінну t за формулою: х=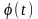 . Якщо функція х= задовольняє умову :

1. х= і 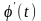неперервна на

2. 

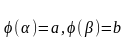
Якщо неперервна на відрізку [ ], то має місце формула:

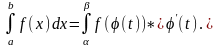
69.Інтегрування частинами у визначеному інтегралі

Якщо функції u(x) і v(x) мають неперервні похідні на відрізку [a, b], тo

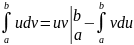
70. Площа плоскої фігури рівняння границі якої задано в декартових координатах і параметрично

Нехай на відрізку [a, b] задана неперервна функція f(x) ≥ 0. Площа криволінійної трапеції − фігури, обмеженої кривою y = f(x), віссю Ox і прямими x = a, x = b, знаходиться за формулою:

S=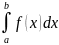

Якщо на відрізку [a, b] функція f(x) ≤ 0 (рис. 2.8), то площа фігури,обмежена віссю Ox, кривою y = f(x) і прямими x = a, x = b обчислюється за формулою:

S=-

71. Площа криволінійного сектора.

S=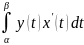

72. Довжина дуги кривої, заданої у декартових координатах.

Нехай на відрізку [a, b] плоска крива задана рівнянням y = f(x),де f(x) − неперервна разом із похідною функція. Тоді довжина дуги АВ обчислюється за формулою:

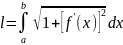
73. Довжина дуги кривої, заданої параметрично й у полярній системі координат

Довжина дуги просторової лінії, заданої параметричними рівняннями x = x(t), y = y(t), z = z(t) (α ≤ t ≤ β), де x(t), y(t),z(t) − неперервно диференційовані на [α, β] функції, обчислюється за формулою:

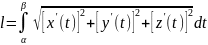
Довжина дуги кривої, що задана рівнянням у полярних координатах ρ = ρ ( ) (α ≤ ≤ β), де ρ( ) і ρ′( ) неперервні на відрізку [α, β], обчислюється за формулою: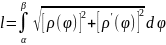

74. Обчислення об’єму тіла по відомих площах його поперечних перерізів. Об’єм тіла обертання

Нехай площа перерізу деякого тіла площиною, перпендикулярноюдо осі ox, подана у вигляді S = S(x), де x [a, b]. Тоді об’єм частини тіла, укладеної між площинами x = a і

x = b, обчислюється за формулою: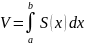

Об’єм тіла, утвореного обертанням навколо осі Оx криволінійної трапеції, обмеженої неперервною на відрізку [a, b] кривою y= f(x), віссю Оx і прямими x = a і x = b, обчислюється за формулою:

75. Невласні інтеграли І роду. Збіжність 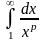. Теореми порівняння.

При визначенні визначеного інтегралу ми припускаєм, що ф-ція f(x) неперервна, а а і b – скінченні числа. Якщо порушена хоч би 1 із цих умов, то інтеграл наз. невласним. Є невласні інтеграли І роду – з нескінченними межами інтегрування від неперервних ф-цій; ІІ роду – з скінченними межами інтегрування від розривних ф-цій.

Означення. Нехай ф-ція f(x) визначена на [a; ∞] і інтегровна на любому відрізку [a; t], t>a, тобто існує 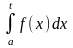при любому t>a. Тоді якщо існує границя lim і дор. скінченному числу, то її наз. невласним інтегралом І роду. Позначається - 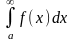(1), тобто 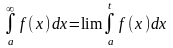(2).

Якщо в (2) він існує, то кажуть, що (1) збігається. Якщо (2) – не існує або дор. ∞, то кажуть, що (1) – є розбіжним.

Аналогічно введем поняття невласного інтегралу 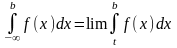(3)

Інтеграл є збіжним, якщот він існує і дор. скінченному числу. Ні – незбіжний.

(4)

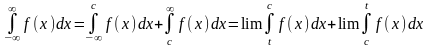
Інтеграл (4) є збіжним, якщо обидва інтеграли в правій частині (4) збіжні, і є розбіжним, якщо хоч би 1 з них є розбіжним.

Теореми порівняння:

Якщо f(x) i g(x) – неперервні на [a; ∞), f(x)≥0 i f(x)≤g(x), то –

1. Якщо 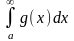- збіжний, то - теж збіжний.

2. Якщо - розбіжний, то - теж розбіжний.

3. Якщо 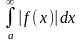- збіжний, то - збігається абсолютно.

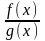4. Якщо lim = k, 0<k<∞, то i одночасно є збіжними або розбіжними.

76. Невласні інтеграли ІІ роду. Збіжність 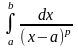. Теореми порівняння.

Якщо ф-ція f(x) неперервна на ]a; b], має нескінченний розрив в т. х=а, тобто lim f(x)=±∞, то тоді вважають, що інтеграл 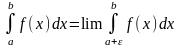, (ε>0) (5)

(5) наз. збіжним, якщо існує скінченна границя в правій частині рівності(5) і наз. розбіжним, якщо дана границя не існує або дор. ∞.

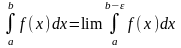, (ε>0) (6)

Якщо ф-ція f(x) неперервна на [a; b], крім т. с (має нескінченний розрив в т.с) (a≤x<c i c<x≤b), тоді –

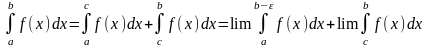(7)

Інтеграл (7) є збіжним, якщо кожний з інтегралів правої частини рівності (7) є збіжним, і розбіжним, якщо хоч би 1 з них інтегралів є розбіжним.

Теореми порівняння.

Якщо ф-ці] f(x) i g(x) неперервні на ]a; b], f(x)≥0, f(x)≤g(x)

1. 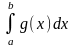- збіжний, то і - збіжний.

2. - розбіжний, то і - розбіжний.

3.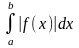 - збіжний, то і - збіжний.

4. lim 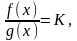0<K<∞, i - одночасно збіжні чи розбіжні.