52.Екстремум ф-ї. Необхідна умова існування екстремуму. (Теорема Ферма).

Означення: точка х₀ із області визначення y=f(x) називається точкою min(max) цієї ф-ї , якщо знайдеться дельта окіл в точці х₀ , що для всіх х, що не співпадають із х₀ з цього околу виконується рівність: f(x₀)<f(x), [f(x₀)>f(x)]. Точки Min(max) називаються точками екстремуму. А значення ф-ї в цих точках екстремумом ф-ї. Теорема Ферма: якщо ф-я y=f(x) диференційована в точці х₀ і її околі, а точка х₀ –є точкою екстремуму цієї ф-ї, то похідна в точці х₀=0.Необхідна умова існування екстремумів в більш загальному вигляді формулюється так: якщо ф-я y=f(x) визначена в околі точки х₀ за виключенням може самої точки х₀, має в точці х₀ екстремум, то похідна в цій точці дорівнює нулю або нескінченості. Означення: точки, в яких перша похідна =0, або не існує називаються стаціонарними або критичними точками першого роду. Необхідна умова існування похідної це:

f^/(х)=0 або f^/(х)=+-нескінченості.

56. Достатні умови екстремуму функції однієї змінної.

Перша достатня умова існування екстремуму функції.

Теорема. Якщо ф-ція y=f(x) неперервна в т. х_о і деякому δ-околі цієї т., має похідну, крім, може, в самій т. х_о , тоді –

1. Якщо f’(x) при переході через т. х_о змінює знак з + на - , то х_о - т. максимуму.

2. Якщо f’(x) при переході через т. х_о змінює знак з – на + , то х_о - т. мінімуму.

3. Якщо f’(x) при переході через т. х_о знак не змінює, то х_о не є т. екстремуму.

Доведення. Нехай f’(x) змінює знак з + на – при переході через т. х_о . Покажемо, що т. х_о - т. максимуму.

Якщо похідна змінює свій знак, то це означає, що існує δ>0 (δ-окіл т. х_о ), що

f’(x)>0 для любого х є [х_о - δ; х_о ]

f’(x)<0 для любого х є [х_о ; х_о + δ].

це означає, що на [х_о - δ; х_о ] ф-ція зростає, на [х_о ; х_о + δ] – спадає. Звідси випливає, що зн-ня ф-ції в т. х_о , яке існує в силу неперервності ф-ції в т. х_о є найбільшим на [х_о - δ; х_о +δ]. Отже, т. х_о - т. максимуму.

Друга достатня умова існування екстремуму ф-ції.

Теорема. Якщо ф-ція y=f(x) визначена і двічі диференційована в деякому околі т. х_о , причому f’(x)=0, а f’’(х_о )≠0, то в т. х_о ф-ція

1. має максимум, якщо f’’(х_о )<0

2. має мінімум, якщо f’’(х_о )>0

3. Доведення. Для визначеності будемо вважати, що f’’(х_о )<0. За означенням lim 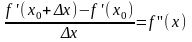. але за умовою теореми f’(x)=0, тоді lim . За припущенням f’’(х_о )<0

. Тоді із означення границі випливає, що в околі деякої т. х_о маємо y’’= lim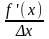 <0, <0. Дослідимо цей дріб на знак в залежності від ∆х. y’’<0, коли в чисельнику і знаменнику будуть різні знаки.

y’’(х_о )= lim . <0 - a) ∆f’(x)<0, ∆x>0 → x>х_о

b) ∆f’(x)>0, ∆x<0 → x<х_о .

Таким чином, в т. х_о ф-ція має максимум.

53.Найбільше і найменше значення ф-ції на відрізку.

Нехай ф-ція у=f(x) неперервна на відрізку [a,b] диференційована в кожній точці цього відрізка і має скінченне число критичних точок 1 роду на цьому відрізку.Необхідно знайти найб. та найм. Значення ф-ції на [a,b].

а)у=f(x) – монотонна (спадна або зростаюча), то найб. і найм. значення вона досягає на кінцях відрізку.

б)у=f(x) не є монотонною, то свого найб. і найм. значень на відрізку [a, b] вона може досягати в одній із критичних точок, що належ. даному відрізку.Для того, щоб знайти значення ф-ції необхідно:

1.Знайти критичні точки 1 роду.

2.Знайти значення ф-ції в критичних точках, що належать відрізку [a,b] і на кінцях відрізка.

3.Вибрати із одержаних значень найб. і найм.

Знаходження найб. і найм. значень ф-ції застосовується при рішенні багатьох практичних задач.