1.Матриця та їх види.Означення дії над ними.

Матрицею порядка М*N наз. прямокутна табл., що складається з MN чисел,які розсташованні m-рядках і n-стовпцях.Означ. матр. Великими буквами А,В,С, а їх елементи-маленькими з подвійною індексацією a i j.Причому перший індекс вказує на № рядка,а Другий-на № стовпця в яких розсташованні ел. a і j.

Види матр.:

1.Квадратна-кількість рядків дорівнює кільк. стовпців.

2.Стовпова-матр. має 1 стовпець .

3.Рядок-має 1 рядок.

4.Нульова матр.-це матр., ел. якої дорівнюють 0.

5.Діагональна-матр. в якій всі ел. розсташованні поза гол. діагон. =0, а хоч би 1 із ел., що стоїть на гол. діагон. відмінний від 0.

6.Одиничною-квадратна матр. в якій всі ел. гол. діагон. =1,а решта =0.

7.Трикутною(верхньотрик.,нижньотрик.)-матр. у якої всі ел.,що розсташованні вище(нижче) гол. діагон. =0.

8.Транспонованна матр.-наз по відношенню до матр А,якщо замінити рядки матр. А її стовпцями або навпаки.

9.Симетричною-якщо при транспонуванні вона не змінюється .

Дві матр. наз. рівними, якщо вони одного розміру і відповідні ел. цих матр. рівні.

Під лін. операціями над матр.розуміють:

а).операція додавання-визначається для матр. одного порядка.

Під сумою(різницею) 2х матр. А(m*n) i B(m*n) розуміють матр. С(m*n), кожний елемент якої дорівнює сумі(різниці) відповідних ел. матр. А, В.

б).Операція множення матр. на число λ полягає в множенні кожного ел. матр. А на це число.

в).Операція множ 2х матр.

А і В визначена в тому випадку , коли кільк. стовпців 1ї матр. співпадає з кільк рядків 2ї матр.

Добутком 2х матр. А(m*k) i B(k*n) розуміють матр. С(m*n), кожний ел. якої = сумі добутків ел. і-го рядка матр.А на відповідні ел. j-го стовпця матр.В.

2.Визначники квадратних матр. та їх властивості.

Кожній квадратній матр. можно поставити у відповідність число, що наз. визначником (детермінантом) і обчислити за певними правилами.Познач.∆

Властивості:

1).вел. визн. не змінюється від заміни рядків його стовпцями(транспонування матр. її визн. не змінює)

2).вел. визн. від перестановки 2х його паралельних рядків (стовпців) змінює знак на протилежний.

3).визн. з 2ма однаковими паралельними рядками =0.

4).спільний множник з ел. ряду можно винести за знак визн.

5).величина визн. не зміниться, якщо до ел. одного ряду +ел. паралельного ряду, попередньо домноживши на деяке число.

3.Визначник, мінор, алгебраїчне доповнення. Властивості визначників. Теорема про розкладання визначника по елементах рядка (стовпця). Обчислення визначників 2-го, 3-го і n-го порядків

Кожній квадратній матр. можно поставити у відповідність число, що наз. визначником (детермінантом) і обчислити за певними правилами.Познач.∆

Властивості:

1).Вел. Визн. Не змінюється від заміни рядків його стовпцями(транспонування матр. Її визн. Не змінює)

2).вел. визн. від перестановки 2х його паралельних рядків (стовпців) змінює знак на протилежний.

3).визн. з 2ма однаковими паралельними рядками =0.

4).спільний множник з ел. ряду можно винести за знак визн.

5).величина визн. не зміниться, якщо до ел. одного ряду +ел. паралельного ряду, попередньо домноживши на деяке число.

Розглянемо матр. n-го порядку А(п*п). Поставимо їй у відповідність визначник n-го порядку.

У визн. n-го порядку довільним способом виділемо ел. аij i викрислемо і-й рядок і j-й стовпець.Тобто той рядок і той стовпець на перетину яких знах. ел. аij .В рез. Одержимо визн.(п-1)го порядку,який назвимо мінором для ел. аij. Аij=(-1) Мij

Теорема Лапласа(про розклад визн. за ел. якого-небудь ряду)

Визн. п-го порядку=сумі попарних добутків ел. якого-небудь рядка(стовпця) на їх алгебраїчні доповнення. ∆=

4.Ранг матр.Способи знаходження.Властивості.

Рангом матр. наз. найвищий порядок мінорів цієї матр.,якщо серед них є не нульовий.

Існують 2 способи знах. рангів:

1).Метод оточуючих мінорів(переход від мінорів нижчих порядків до мінорів більш високих порядків).

2).Елементарних перетворень

Властивості:

1.rgA<= min(m,n)

2.rgA=0, то А- нульове

3.якщо rgA квадратної матр.=її порядку. то визн. цієї матр. відмінний від 0

а).ранг матр. не змінеться, якщо протранспонувати матр.

б).поміняти місцями 2 паралельні ряди

в).викреслити нульовий ряд

г)домножити ел. якого-небудь ряду на довільне число відмінне від 0.

д).до ел. одног ряду додати ел. паралельного ряду попередньо домноживши їх на деяке число.

5.Обернена матриця.Алгоритм обчислення.

Матриця А наз. оберненою до матр. А, якщо викон. Співвідношення А*А =Е*(А *А)=Е

Теорема про існування оберненої матр.:для всякої неособливої квадратної матр. існує обернена,яка обчислюється за певною формулою:А =А /∆

Алгоритм обчислення:

1.Знайти визначник матр. А,∆≠0

2.Знайти алгебраїчні доповнення до ел. матр. і скласти союзну матр., ел. якої є алгебраїчні доповнення Аij=(-1) Mij

3. Протранспонувати матр.

4.Елементи союзної транспонованої матр. поділити на величину визначника.

5.Зробимо перевірку: А*А =Е*(А *А-Е)

6.Розв’язання слар за формулами Крамера.

Якщо головний визначник, складений з коефіцієнтів при невідомих, системи n-лінійних рівнянь з n-невідомими відмінний від нуля, то така система рівнянь має єдиний розв’язок (сумісна і визначена), який знаходиться за формулами:

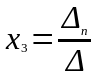, , ..., .де -головний визначник, який складається з коефіцієнтів при невідомих у лівій частині системи.

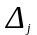-визначник, який одержується шляхом заміни j-го стовпчика в головному визначник на стовпчик вільних членів.

7.Система лінійних алгебраїчних рівнянь.Основні поняття і визначення.Теорема Кронекера-Капеллі.

Розв‘язком системи наз. сукупність чисел х ,х ,...х ,які при підстановці в систему кожне рівняння перетворять в тотожність.Система може мати, а може і не мати розвязок.Якщо система має розвязок-сумісна, не має-не сумісна, єдиний розвязок-наз визначеною,безліч-невизначеною.

Теорема Кронекера-Капеллі-для того,щоб система лінійних рівнянь була сумісною, необхідно і достатньо, щоб ранг її основної матр.= рангу розширеної матр.Якщо ранг основної матр. дорівнює рангу розширеної матр. і дорівнює числу невідомих системи, то система має 1 розвязок.Якщо ранг основної матр.=рангу розширеної матр., але менший від числа невідомих системи, то система має безліч розвязків.