1. 6 Оценочная функция

Оценочная функция (ОФ) ставит в соответствие позиции на доске некое число, отражающее выгодность этой позиции для игрока в условных единицах. Не суть важно, что это за единицы, главное, чтоб их можно было сравнивать друг с другом.

Будем полагать, что оценочная функция – симметричная, т.е. если белые “думают”, что они находятся в хорошей позиции, то черные “полагают”, что они на столько же в плохой позиции.

ОФ – может быть более или менее сложная, в зависимости от встроенных в нее знаний. Соответственно, чем более сложная ОФ, тем дольше ее вычислять. Обычно производительность программы (т.е. насколько она хорошо играет) может быть оценена как произведение “скорости” на “знание”.

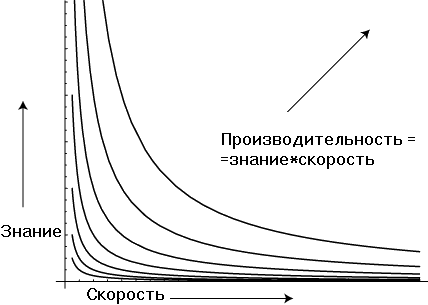
Рис. 4 Оценочная функция.

В качестве оценочной функции используются линейные модели (линейная комбинация некоторых параметров).

В простейшей модели в качестве параметров можно взять просто количество фишек на каждом поле, получив в сумме 26 параметров. Реально же используют некоторые вычисляемые параметры, представляющие определенные стратегические аспекты игры.

Одним из основных параметров является подсчет пипсов – это число, которое нужно выбросить на игральных костях, чтобы вывести все свои фишки. По этому параметру определяют лидерство и близость победы.

Число одинарных фишек также является важным параметром, который стремятся сокращать все игроки, так как только одинарные фишки можно побить в нардах, тем самым откинув противника в гонке за вывод фишек из доски.

Число полей с двумя и более фишками является противоположностью предыдущему параметру, его стремятся максимизировать. Чем больше таких полей, тем устойчивее позиция и тем сложнее через нее пройти.

Связанным параметром является построение блокад – несколько смежных полей, занятых двойными или более фишками. С этим параметром можно связать изменение стратегии – нужно проводить свои фишки вперед, если их запирают.

Также считают число прямых возможностей взятия – это число одинарных фишек на расстоянии 6 или меньше полей. Есть схожий с этим параметр – число одинарных фишек на расстоянии меньшем 12. Схожим параметром является вероятность взятия одинарной фишки, которая в большинстве случаев рассчитывается по предварительно посчитанной таблице.

Равномерность распределения фишек по полям. Например, гораздо выгоднее иметь три фишки на одном поле и еще три на другом, чем две и четыре на тех же полях. В случае выпадения определенных костей может потребоваться сдвинуть фишку с первого поля и тем самым сделать как минимум одну одинарную фишку.

Анализируя сыгранные партии можно заметить, что занятие определенных позиций на доске способствует победе. Такими позициями является 4-я и 5-я клетки и соответственно 20-я и 21-я симметричные клетки. Таким образом, в простейшем случае можно ввести факт занятия этих клеток в оценочную функцию. В более общем случае, вводят весовые коэффициенты для всех полей доски.

Также часто используется параметр коммуникации – нужно стремиться располагать свои фишки на расстоянии не более 6 пипсов друг от друга. Тем самым препятствовать разделению своих фишек.

При выводе своих фишек, нужно стремиться оставлять четное число фишек на каждом поле, чтобы минимизировать шансы оставления одиночной фишки после очередного хода.

Очень часто вводятся понятия контакта фишек – наличие хотя бы одной вражеской фишки в направлении движения. Наличие факта контакта влияет на используемую стратегию и может предполагать разные оценочные функции.

Эвристический метод, используемый для получения подобных оценок, в общем, заключается во введении некоторой числовой функции на множестве позиций, зависящей от ряда переменных, которую называют оценочной функцией (evaluation function). Переменными, обычно служат разного рода элементарные оценки позиции, такие как, например, материальный перевес, пешечные структуры, угрозы фигурам. Функция должна быть легко вычисляема, поэтому её обычно строят в виде линейной функции соответствующих переменных. Некоторые исследователи ищут развитие этого метода в усложнении вида оценочной функции путем введения в нее нелинейных элементов или использования булевых функций. Тем не менее, сложность расчета такой функции имеет критическое значение, так как должна быть оправдана отказом от исследования дальнейшего развития ситуации. Иными словами, время, потраченное на вычисление слишком сложной оценочной функции, может быть с гораздо большим успехом потрачено на просчет ходов из данной позиции, и расчет более простой оценочной функции в полученных позициях.

Так или иначе, оценочная функция определяется набором переменных, видом, и набором параметров. Выбор переменных производится путем анализа экспертных знаний. На этом этапе иногда есть возможность обратиться к литературе по теории данной игры, каковой в избытке можно найти по шахматам. Кроме того, на практике часто очень полезны даже самые элементарные соображения экспертов, имеющих опыт игры. Это очень важно в случае с играми, для которых не создано такой внушительной теоретической базы. В некоторых, достаточно простых играх хватает всего трех переменных, и такая функция делает игру программы сносной; в шахматах их число обычно достигает нескольких сотен. Вид функции, как уже говорилось, определяется сравнительной легкостью вычисления. Последним этапом построения оценочной функции, а зачастую и всей программы, является подбор параметров при переменных (нелинейных или булевых слагаемых), то есть весов соответствующих критериев оценки позиции. Здесь анализа экспертных знаний всегда недостаточно. Часто критерии кажутся несоотносимыми, хотя требуют точнейшей сравнительной оценки. Большое количество переменных, а соответственно и параметров, делает более-менее адекватный их априорный выбор просто невозможным. Еще одна проблема при выборе параметров - их нестабильность в том смысле, что в разных фазах игры, а иногда и в разных игровых ситуациях, наиболее сильной игре соответствуют разные оценочные функции. Может появиться необходимость в течение игры менять как параметры оценочной функции, так и её структуру. В случае с фазами игры можно заранее предусмотреть такую замену, а в случае с различными игровыми ситуациями (которых на практике может оказаться больше, чем в теории) потребуется в процессе игры выбирать адекватную программу. Причем существуют варианты: выбирать из готовых, и/или адаптировать существующую программу, получая новую. Эта частная задача относится к классу задач самообучения игровых программ, который подробнее рассматривается ниже.

Учитывая то, что прочие аспекты построения программ, играющих в сложные позиционные игры (такие как порядок обхода дерева игры и построение частичных оценок позиций), довольно тщательно изучены, и результаты соответствующих исследований широко применяются, можно полагать, что решающую роль в написании таких программ в настоящее время играет именно нахождение наилучшей процедуры выбора оценочной функции. Данная работа рассматривает некоторые проблемы связанные с задачей подбора параметров в оценочной функции на этапе, когда её вид и набор переменных уже заданы (либо существует несколько вариантов таковых).