3.2 Использование нейронных сетей в качестве оценочной функции.
Для применения нейронных сетей в качестве оценочной функции нужно определить ее топологию, сформировать обучающую выборку и обучить.
Большинство авторов склоняется к использованию трехслойной нейронной сети (MLP) как наиболее удобной в данном случае, такие сети были использованы и в этой работе. Существует несколько подходов к определению числа нейронов в каждом слое. Например, входные нейроны можно понимать как позицию на доске, представленную в некотором виде (26 входов по числу полей на доске), либо уже посчитанные параметры от эвристической оценочной функции, либо совмещение этих вариантов.
В качестве данных для обучения могут быть применены: база партий признанных игроков, выборка с позициями, оцененными эвристической оценочной функцией, выборка с оценкой по числу выигранных партий одним из игроков. Каждый из этих вариантов обладает своими преимуществами и недостатками. Так, база партий признанных игроков может позволить получить хорошие оценки качества позиций, но такие базы отсутствуют в свободном доступе, либо имеют очень ограниченный объем или неопределенное происхождение. Нейронная сеть, обученная по выборке с позициями, оцененными эвристической оценочной функцией (ОФ), не может играть лучше чем исходная ОФ, но может вычисляться быстрее. Наилучших результатов можно добиться используя выборки с оценкой по числу выигранных партий одним из игроков. Для построения такой выборки проводится N партий для некоторого набора позиций (размер выборки), между двумя равными сильными игроками. Причем под числом побед белых над черными можно понимать оценку данной позиции.
3.3 Использование MatLab для обучения нейронных сетей.
Для обучения нейронной сети использовался инструмент nntool программного комплекса МаtLab 7.0. Использование MatLab для обучения нейронной сети может быть объяснено повышенным удобством построения нейронных сетей с помощью инструмента nntool, возможностью визуализации построенной нейронной сети, возможностями значительных вариаций методов обучения нейронных сетей, несколькими способами инициализации весов, наглядным представлением и отсутствием необходимости разрабатывать и отлаживать код обучения НС, и тем самым сокращение сроков разработки готовой программы.
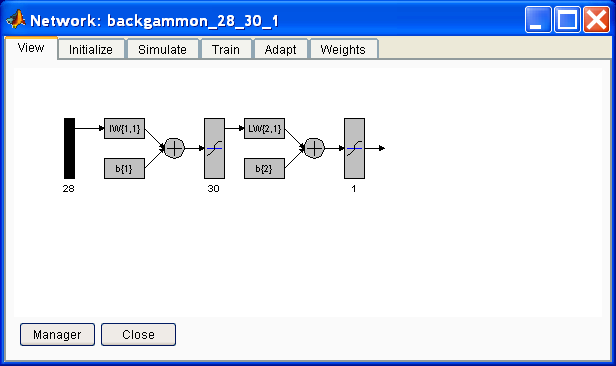
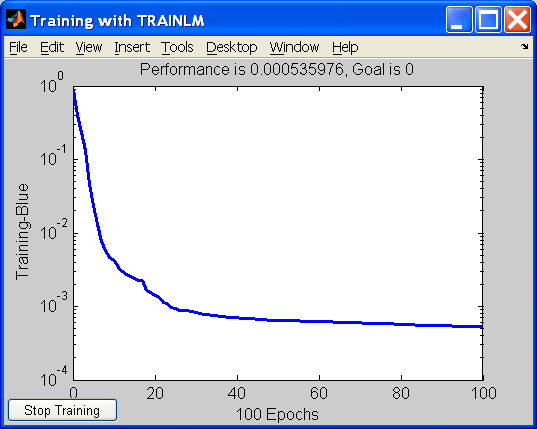
Рис. 2 Графическое представление одной из использовавшихся нейронных сетей и график ошибки обучения сети в инструменте nntool.
В рамках этого подхода была написана программа-экспортер позиций и их оценок из внутреннего представления программы в формат MatLab. Для получения данных (весов нейронной сети) обратно была написана программа-импортер, которая переводит веса обученной нейронной сети из MatLab во внутренний формат программы.
Также была реализована функциональность нейронных сетей в качестве оценочной функции (замена эвристической оценочной функции нейронной сетью производится простой заменой классов в программе).
Для настройки весов нейронных сетей использовался алгоритм обратного распространения ошибки. Суть метода состоит в измерении ошибки между вектором выходных значений нейронов и желаемым выходом, с возвращением получившейся ошибки к входному уровню с целью выбрать веса в связях минимизирующие ошибки на выходном уровне, при помощи алгоритма дельта обучения. В комбинации с этим методом также использовался стахостический метод, основанный на внесении псевдослучайных изменений в величины весов, сохраняя те изменения, которые ведут к улучшениям. Этот метод позволяет обойти такие проблемы как: локальные минимумы и паралич сети. т брать наиболее сильные эвристические функции, для получения правдоподобных оценок вероятности победы иозиций, для работы с большими нт и генерируется некоторое число позиций (в работе использовались выборки размером 10 тыс.