28. Общие индексы и их применение в анализе.

Если известно, что изучаемое явление неоднородно и сравнение уровней можно провести только после приведения их к общей мере, экономический анализ выполняют посредством так называемых общих индексов. Индекс становится общим, когда в расчетной формуле показывается неоднородность изучаемой совокупности. Примером неоднородной совокупности является общая масса проданных товаров всех или нескольких видов. Тогда сумму выручки можно записать в виде агрегата (суммы произведений взвешивающего показателя на объемный), например:

Отношение агрегатов, построенных для разных условий, дает общий индекс показателя в агрегатной форме. Так, например, получают индекс общего объема товарооборота в агрегатной форме:

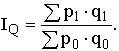
При анализе прироста общего объема товарооборота этот прирост также объясняется изменением уровня цен и количества проданных товаров.

Влияние на прирост товарооборота общего изменения цен выражается агрегатным индексом цен I_p, который в предположении первичности изменения количественного показателя (q) и вторичности – качественного (р) имеет вид

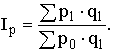
Влияние на прирост товарооборота изменения количества проданных товаров отражается агрегатным индексом физического объема I_q, который строится также в предположении первичности изменения количественных показателей (q) и вторичности влияния качественных (р):

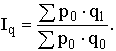
29. Индексы при анализе структурных изменений.

Индексы, которые рассчитываются по типу индексов физического объема, применимы при изучении совокупностей, состоящих как из разных объектов, так и из объектов одного и того же типа. Если совокупность неоднородна (например, совокупность товаров различного вида), то индекс физического объема – единственный способ показать динамику такой массы различных предметов, выражая ее через взвешивающий множитель (цену, себестоимость, трудоемкость). Если же совокупность состоит из объектов одного типа, то динамику этой массы можно показать непосредственно, сравнивая общее количество таких предметов в отчетном периоде с аналогичной величиной в базисном.

Таким образом, для однородных совокупностей (допускающих суммирование по количественному признаку) индекс физического объема есть произведение индекса суммарной численности  совокупности на индекс изменения структуры. Формула индекса структурных  изменений может быть такова:

где d₀ – удельные веса, например доли предприятий в общей численности работающих в базисном периоде, a d₁ – удельные веса или доли каждого предприятия в общей численности работающих в отчетном периоде:

Знаменатель в формуле  индекса структурных изменений  есть не что иное. как средний уровень (выработки по группе предприятий) в базисном периоде, так как

Экономическая сущность индекса  структурных изменений состоит  в том, что он показывает, во сколько  раз изменился общий средний  уровень только за счет изменения  удельного веса каждого объекта  в общем объеме количественного  признака. В той же мере индекс структурных изменений показывает влияние процессов перераспределения на общий прирост итогового показателя.

В итоге в форме мультипликативной  индексной модели можно записать:

Общий прирост продукции  состоит, следовательно, из трех частей:

1) прирост за счет изменения  общей численности работающих

2) прирост за счет перераспределения  работающих

3) прирост за счет изменения  уровня производительности труда  на предприятиях

Вклад разных факторов в  общий прирост можно распределить по отдельным объектам, для каждого  из которых применяют мультипликативную  индексную модель

где q₀, q₁, – объемы итогового признака (продукции) по данному объекту (предприятию);  I _{sum T} – общий для всей совокупности индекс количественного признака (индекс числа работающих);  i_W – индивидуальный для данного объекта индекс изменения уровня качественного признака (индивидуальный индекс производительности труда для данного предприятия);  i_d – индивидуальный индекс доли данного объекта в общем объеме количественного признака (индивидуальный индекс доли данного предприятия в общей численности работающих).