13. Законы распределения дискретных случайных величин: биномиальное, Пуассона, геометрическое, гипергеометрическое.

Биномиальное распределение. Пусть производится n независимых испытаний, в каждом из которых событие А наступает с постоянной вероятностью р (вероятность ненаступления q=1-p).

Биномиальным распределением дискретной случайной величины Х называется распределение вероятностей, определяемое формулой Бернулли

Р аспределение Пуассона. Если число испытаний вероятность , при этом сохраняет постоянное значение, то для вычисления вероятностей в схеме Бернулли используется асимптотическая формула Пуассона.

Д ля биномиального распределения справедливы следующие утверждения:

Для распределения Пуассона с параметром справедливы утверждения:

Геометрическое распределение. Пусть производятся независимые испытания, в каждом из которых событие А наступает с постоянной вероятностью р (вероятность ненаступления q=1-p). Испытания заканчиваются, как только наступит событие А.

Вероятность того, что событие А появилось в к-ом испытании ( в предшествующих

( к-1) испытаниях оно не появилось)

14. Законы распределения непрерывных случайных величин: равномерное, показательное, нормальное. Распределения, связанные с нормальным: «хи-квадрат», Стьюдента, Фишера.

Р авномерное распределение. Распределение вероятностей называют равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение:

-постоянная положительная величина.

П оказательное распределение. Показательным распределением непрерывной случайной величины называется распределение, плотность которого имеет вид:

Н ормальным называют распределение вероятностей непрерывной случайной величины, которое задается функцией плотности вида:

Н ормальное распределение определяется двумя параметрами и , вероятностный смысл которых таков: есть математическое ожидание, а - среднее квадратическое отклонение нормального распределения.

Р аспределение («хи-квадрат»). распределена по закону с степенями свободы.

Р аспределение Стьюдента ( t - распределение). Пусть Z -нормально распределенная случайная величина, причем математическое ожидание Z равно нулю, среднее квадратическое отклонение равно единице. Пусть V – независимая от Z случайная величина, распределенная по закону с k степенями свободы.

Тогда величина имеет распределение Стьюдента с k степенями свободы.

Р аспределение Фишера ( F - распределение). Пусть U и V -независимые случайные величины, распределенные по закону со степенями свободы Тогда величина имеет распределение Фишера со степенями свободы .

15. Нормальное распределение и его свойства. Правило трех сигм. Вероятность попадания в заданный интервал нормальной случайной величины. Асимметрия и эксцесс нормального распределения.

Стандартным нормальным(нормированным) называют нормальное распределение с параметрами

Плотность стандартного нормального распределения имеет вид:

Ф ункция распределения нормированного распределения:

График плотности нормального распределения называют нормальной кривой (кривой Гаусса). Нормальная кривая имеет симметричный «колоколообразный» вид.

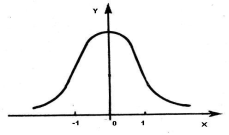
Свойства нормального распределения.

1. Функция определена на всей числовой оси .

2. При всех значениях х функция принимает положительные значения, т.е. нормальная кривая расположена над осью ОХ .

3.Ось ОХ служит горизонтальной асимптотой графика.

4 .При функция имеет максимум, равный

5. График функции симметричен относительно прямой

8. Вероятность попадания нормальной случайной величины Х в произвольный интервал равна

«Правило трех сигм»: вероятность того, что отклонение по абсолютной величине меньше утроенного среднего квадратического отклонения, равна 0,9973.

16. С истемы случайных величин. Функция распределения и плотность распределения двумерной случайной величины. Коррелированность и зависимость случайных величин. Коэффициент корреляции. Корреляционный момент. Уравнение регрессии. Метод наименьших квадратов.

У порядоченная совокупность случайных величин , рассматриваемых совместно, называется n-мерной случайной величиной или системой случайных величин.

Двумерную случайную величину геометрически можно интерпретировать как случайную точку на плоскости. Случайные величины X и Y называются независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина. В противном случае величины X и Y называются зависимыми.

К орреляционным моментом (ковариацией) случайных величин X и Y называется математическое ожидание произведения отклонений этих величин :

К орреляционный момент двух независимых случайных величин X и Y равен нулю.

Коэффициентом корреляции случайных величин X и Y называется отношение корреляционного момента к произведению средних квадр отклонений этих величин:

Две случайные величины X и Yназываются коррелированными, если их коэффициент корреляции (или корреляционный момент отличен от нуля); X и Y называются некоррелированными, если их коэффициент корреляции равен нулю.