
- •П ерестановки. Размещения. Сочетания.
- •Случайные события. Операции над событиями.
- •Определения вероятности: классическое, статистическое, аксиоматическое. Геометрическая вероятность.
- •Теоремы сложения и умножения вероятностей. Условная вероятность. Независимость событий.
- •Ф ормула полной вероятности. Формула Байеса.
- •Повторные независимые испытания. Схема испытаний Бернулли. Формула Бернулли. Формула Пуассона.
- •Локальная и интегральная теоремы Лапласа
- •В ероятность отклонения относительной частоты от постоянной вероятности. Наивероятнейшее число наступлений события.
- •Случайные величины: дискретные и непрерывные. Закон распределения.
- •Функция распределения вероятностей и ее свойства.
- •Плотность распределения вероятностей и ее свойства.
- •Числовые характеристики дискретных и непрерывных случайных величин, их свойства
- •Законы распределения дискретных случайных величин: биномиальное, Пуассона, геометрическое, гипергеометрическое.
- •Законы распределения непрерывных случайных величин: равномерное, показательное, нормальное. Распределения, связанные с нормальным: «хи-квадрат», Стьюдента, Фишера.
- •Закон больших чисел. Неравенство и теорема Чебышева. Теорема Бернулли. Теорема Пуассона.
- •Генеральная и выборочная совокупности. Статистические ряды. Полигон и гистограмма . Эмпирическая функция распределения.
- •Статистические оценки. Несмещенные, эффективные и состоятельные оценки.
- •Точечные оценки. Генеральное среднее. Генеральная дисперсия. Выборочное среднее. Выборочная дисперсия. Исправленная выборочная дисперсия. Мода, медиана, размах вариационного ряда.
- •Доверительный интервал для оценки дисперсии нормального распределения.
П ерестановки. Размещения. Сочетания.
П ерестановкой
из n
элементов называется число способов,
при помощи которых можно расположить
n
различных элементов на n
различных местах.
ерестановкой
из n
элементов называется число способов,
при помощи которых можно расположить
n
различных элементов на n
различных местах.
Р азмещением
из n
элементов по m
называется число способов, при помощи
которых можно расположить m
различных элементов на m
различных местах, выбранных из n.
азмещением
из n
элементов по m
называется число способов, при помощи
которых можно расположить m
различных элементов на m
различных местах, выбранных из n.
C очетанием
из n
элементов по m
называется число способов, при помощи
которых можно выбрать m
различных элементов из данных n
элементов.
очетанием
из n
элементов по m
называется число способов, при помощи
которых можно выбрать m
различных элементов из данных n
элементов.
Случайные события. Операции над событиями.
События, происходящие вокруг нас, можно разделить на 3 вида: достоверные, невозможные и случайные.
Достоверным называется событие, которое неизменно происходит при выполнении некоторого комплекса внешних условий.
Невозможным называется событие, которое заведомо не происходит при выполнении некоторого комплекса внешних условий.
Случайным называется событие, которое может либо происходить либо не происходить при выполнении некоторого комплекса внешних условий.
Суммой событий A и B называется событие A+B такое, что наступит событие А, либо наступит событие B , либо оба вместе.
Произведением событий А и B называется событие AB такое, которое происходит при одновременном наступлении событий А и B.
Событием, противоположным событию B) называется такое событие, при котором не происходит событие B.
Р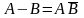 азностью
событий А и B
называется такое событие, которое
состоится, если событие А произойдет,
а событие B
не произойдет.
азностью
событий А и B
называется такое событие, которое
состоится, если событие А произойдет,
а событие B
не произойдет.
Два события называются совместными, если наступление одного из них не исключает наступление другого в том же испытании. Два события называются несовместными, если их совместное наступление невозможно.
Определения вероятности: классическое, статистическое, аксиоматическое. Геометрическая вероятность.

(классическое). Вероятностью Р(А) события А называют отношение где n – общее число всех возможных элементарных исходов испытания; m – число возможных элементарных исходов, благоприятствующих событию А.
Элементарными событиями, благоприятствующими событию А, называют элементарные события, входящие в состав события А.
(

 статистическое).
За вероятность Р(А) события А принимают
отношение числа испытаний, в которых
наступило событие А, к общему числу
произведенных испытаний
или
статистическое).
За вероятность Р(А) события А принимают
отношение числа испытаний, в которых
наступило событие А, к общему числу
произведенных испытаний
или
Величину называют относительной частотой события А.
Утверждение. Относительные частоты обладают свойством устойчивости.
(

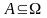 аксиоматическое).
Пусть
-
множество элементарных событий.
,
аксиоматическое).
Пусть
-
множество элементарных событий.
,
Определим на множестве неотрицательную меру, называемую вероятностью, со свойствами:
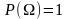 (вероятность
достоверного события равна единице);
(вероятность
достоверного события равна единице);
 (вероятность
невозможного события равна нулю);
(вероятность
невозможного события равна нулю);для любого события А;
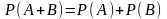 если
А и B
– несовместные события
если
А и B
– несовместные события
О пределение
4 (геометрическое).
Вероятность попадания в область g
при бросании точки наудачу в область G
равна
пределение
4 (геометрическое).
Вероятность попадания в область g
при бросании точки наудачу в область G
равна
где mes – мера области ( длина, площадь, объем).
