2.1.2. Режимы работы
Если в уравнении механической характеристики (2.7) изменять напряжение в интервале (+Uн,−Uн), то при различных значениях скорости и момента мы получим семейство механических характеристик, расположенных во всех четырех квадрантах плоскости параметров ω,M (рис. 2.4). В квадрантах 1 и 3 имеем двигательный режим, так как здесь электромагнитная мощность двигателя положительна – P=Mω>0, а в квадрантах 2 и 4 реализуются тормозные (генераторные) режимы, так как здесь P<0. Причем, если двигательный режим один (область его существования отмечена горизонтальной штриховкой), то тормозных режимов несколько. Рассмотрим их.
Из теории электрических машин известно, что генераторный режим имеет место в том случае, если э.д.с. и ток двигателя одного знака. Согласно (2.4) имеем
(2.15)
Iя=(U−E)/Rя.
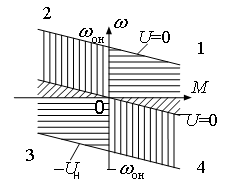
Рис. 2.4. Области существования режимов работы привода
Отсюда можно заключить, что ток и э.д.с. будут одного знака в трех случаях:
если при одинаковых знаках, модуль э.д.с. больше модуля напряжения на якорной обмотке |E|>|U|;
если напряжение якорной обмотки равно нулю U=0 (при ω≠0);
если напряжение и э.д.с. имеют разные знаки signU=−signE.
Режим, соответствующий первому условию, называют рекуперативным торможением. Он возникает в том случае, если скорость двигателя под действием внешнего момента, возникающего при торможении рабочего органа, превысит скорость холостого хода, т.е. рабочая точка привода по механической характеристике перейдет из квадранта 1 в квадрант 2, либо из квадранта 3 в квадрант 4 (рис. 2.4). Область существования режима рекуперативного торможения отмечена вертикальной штриховкой. При этом двигатель работает как обычный генератор постоянного тока, его механическая и электромеханическая характеристики описываются теми же уравнениями (2.5) и (2.7). Уравнение баланса мощностей имеет вид
(2.16)
Pэ=Pм−ΔP,
где: Pм – механическая мощность, поступающая от рабочего органа, Pэ – мощность, генерируемая двигателем, ΔP – потери мощности в обмотке якоря.
В соответствии с выражением (2.16) механическая энергия торможения рабочего органа частично возвращается в сеть, а частично рассеивается в виде потерь в двигателе.
Режим, соответствующий второму условию называют динамическим торможением. Физически он реализуется путем отключения двигателя от сети и закорачивания обмотки якоря, либо включения ее на добавочное активное сопротивление. В первом случае рабочая точка привода оказывается на линии механической характеристики при U=0, которая является механической характеристикой режима динамического торможения при Rд=0. Во втором случае уравнение механической характеристики двигателя при динамическом торможении имеет вид
(2.17)
ω=−(Rя+Rд)·M/(KΦ)2.
Следовательно, в обоих случаях механические характеристики проходят через начало координат и отличаются только жесткостью.
Уравнение баланса мощностей для динамического торможения имеет вид
(2.18)
Pм=ΔP.
Согласно этому уравнению механическая энергия торможения рассеивается в виде электрических потерь на добавочном сопротивлении и в обмотке якоря.
Режим, соответствующий третьему условию, называют противовключением. Физически он реализуется, если под действием момента со стороны рабочего органа двигатель начнет вращаться в обратную сторону, т.е. рабочая точка перейдет по механической характеристике из квадранта 1 в квадрант 4 или из квадранта 3 в квадрант 2. Режим противовключения возникает также, если в работающем двигателе изменить полярность напряжения на якорной обмотке. Тогда за счет инерции вращающихся частей какое-то время якорь будет вращаться в сторону, противоположную направлению момента. Отсюда и название режима. Область существования режима противовключения отмечена наклонной штриховкой.
Уравнение механической характеристики имеет вид
(2.19)
ω=−(U/(KΦ)+Rя·M/(KΦ)2).
При переключении полярности напряжения в обмотке якоря может возникнуть большой ток, определяемый выражением
Iя=−(U+E)/Rя,
поэтому необходимо предусматривать меры по его ограничению, например, путем введения добавочного сопротивления в цепь якоря или используя устройства ограничения тока в преобразователях напряжения, от которых питается двигатель.
Уравнение баланса мощностей имеет вид
(2.20)
Pм+Pэ=ΔP.
В соответствии с этим уравнением при торможении противовключением механическая энергия торможения и электрическая энергия, потребляемая двигателем, преобразуются в электрические потери.