Системы случайных величин
Существенный интерес в математической статистике представляет рассмотрение системы двух и более случайных величин и их статистическая взаимосвязь друг с другом.
По аналогии с рядом распределения одной дискретной величины Х для двух дискретных случайных величин X и Y строится матрица распределения – прямоугольная таблица, в которой записаны все вероятности pi j = P{ X = xi , Y = yj } , i = 1, … , n; j = 1,…, m.
События (или опыты) называются независимыми, если вероятность появления (исхода) каждого из них не зависит от того, какие события (исходы) имели место в других случаях (опытах).
Две случайные величины X и Y называются независимыми, если независимы все связанные с ними события: например, {X < а} и {Y <b} или {X = xi} и {Y = yi} и т.д.
В терминах законов распределения справедливо также следующее определение: две случайные величины X и Y называютсянезависимыми, если закон распределения каждой из них не зависит от принятого значения другой.
Совместной функцией распределения системы двух случайных величин ( X, Y ) называется вероятность совместного выполнения неравенств X < х и Y < у :
(34)
Событие
означает
произведение (совместное выполнение)
событий {X < х}
и {Y <
у}.
Геометрической
интерпретацией совместной функции
распределения F ( x, y)
является вероятность попадания случайной
точки ( X, Y )
на плоскости внутрь бесконечного
квадранта с вершиной в точке (x, y)
(заштрихованная область на рис. 8).
Рис. 8. Геометрическая интерпретация совместной функции распределения F(x, y)
Основные свойства совместной функции распределения:
(35)
Здесь 
Система
двух случайных величин ( X, Y )
называется непрерывной,
если ее совместная функция
распределения F (x, y)
– непрерывная функция, дифференцируемая
по каждому аргументу, у которой существует
вторая смешанная частная производная 
.
Обе случайные величины X и Y –
непрерывны. Тогда функция
(36)
называется совместной плотностью распределения системы двух случайных величин ( X, Y ).
Основные свойства совместной плотности распределения:
(37)
В качестве числовых характеристик системы двух случайных величин X и Y обычно рассматриваются начальные и центральные моменты различных порядков. Порядком момента называется сумма его индексов k + s.
Начальным моментом порядка k + s системы двух случайных величин X и Y называется математическое ожидание произведения X kна Y s :
(38)
Центральным моментом порядка k + s системы двух случайных величин ( X, Y ) называется математическое ожидание произведения (X–mx )k на (Y–my )s :
(39)
где mx = М (Х), my = М (Y).
Для системы дискретных случайных величин X и Y :
(40)
(41)
где рi j = Р { Х =xi , Y = yj }.
Для системы непрерывных случайных величин X и Y :
(42)
(43)
где f ( x, y ) – совместная плотность распределения случайных величин X и Y.
В инженерных приложениях математической статистики чаще всего используются моменты первого и второго порядков.
Начальные моменты первого порядка
(44)
являются математическими ожиданиями случайных величин X и Y.
Центральные моменты первого порядка всегда равны нулю:
(45)
Начальные моменты второго порядка:
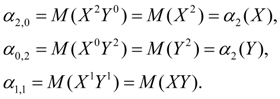(46)
Центральные моменты второго порядка:
(47)
Здесь Dx , Dy – дисперсии случайных величин X и Y.
Центральный
момент второго
порядка 
называется ковариацией случайных
величин X и Y.
Обозначим его 
:
.
(48)
Из определения ковариации (48) следует:
(49)
Дисперсия случайной величины является по существу частным случаем ковариации:
(50)
По определению ковариации (48) получим:
(51)
Ковариация
двух случайных величин X и Y характеризует
степень их зависимости и меру рассеивания
вокруг точки 
.
Часто бывает удобно выразить ковариацию
в
виде:
(52)
Выражение (52) вытекает из определения ковариации (48).
Размерность ковариации равна произведению размерностей случайных величин X и Y.
Безразмерная величина, характеризующая только зависимость случайных величин X и Y, а не разброс:
(53)
называется коэффициентом корреляции случайных величин X и Y. Этот параметр характеризует степень линейной зависимости случайных
величин X и Y.
Для любых двух случайных величин X и Y
коэффициент корреляции 
.
Если 
,
то линейная зависимость
между X и Y возрастающая,
если 
,
то линейная зависимость междуX и Y убывающая,
при 
линейной
зависимости между X и Y нет.
При 
случайные
величины X и Y
называются коррелированными, при
–
некоррелированными. Отсутствие линейной
корреляции не означает отсутствие любой
другой зависимости между X и Y.
Если имеет место жесткая линейная
зависимость Y = aX+ b ,
то 
при а >
0 и 
при а <
0.
31
Функцией
распределения 
двумерной
случайной величины 
называется
вероятность произведения событий 
и 
,
определенная для любых вещественных 
: 
. (1)
Функция 
для
краткости называется двумерной
функцией распределения.
Геометрический
смысл равенства (1): функция
есть
вероятность того, что случайная
точка
попадет
в бесконечный квадрат с вершиной в
точке 
;
точка
будет
левее и ниже этой вершины.
Свойства двумерной функции распределения
1. 
.
2. 
, 
.
3. 
.
4. 
;
.
(2)
5. неубывающая функция по каждому из своих аргументов при фиксированном другом аргументе.
32
Плотность
совместного распределения
вероятностей 
можно
рассматривать как предел отношения
вероятности попадания случайной точки
в прямоугольник (с вершиной в точке 
и
сторонами 
и 
)
к площади этого прямоугольника, когда
обе стороны этого прямоугольника
стремятся к нулю.
Действительно,
вероятность попадания случайной точки
(
, 
)
в прямоугольник с вершинами
, 
, 
и 
равна:
Применив к правой части теорему Лагранжа, получим:
где 
; 
.
Отсюда:
.
Приняв
во внимание, что 
–
площадь рассматриваемого прямоугольника,
можно сделать вывод, что 
–
это отношение вероятности попадания
случайной точки в рассматриваемый
прямоугольник к площади этого
прямоугольника. Если перейти к пределу
при 
и 
,
то 
и 
и,
следовательно, 
.
Аналогично вероятности для дискретной
случайной величины, плотность распределения
вероятности для непрерывных величин
можно представить в виде:
.