- •Дискретные и непрерывные случайные величины
- •Закон распределения дискретной случайной величины
- •Числовые характеристики дискретных случайных величин.
- •Начальные и центральные теоретические моменты
- •Функция распределения случайной величины
- •Плотность вероятности
- •[Править]Свойства плотности вероятности
- •Числовые характеристики случайных величин
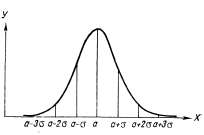
- •Правило трёх сигм
- •Функция надежности. Показательный закон надежности.
- •Система случайных величин
- •Системы случайных величин
- •Нахождение функции распределения по известной плотности распределения
- •[Править]умо относительно σ-алгебры
- •Умо относительно семейства событий
- •Умо относительно случайной величины
- •Условная вероятность
- •Корреляционный момент и коэффициент корреляции.
- •Коррелированность и зависимость случайных величин
- •Корреляционные матрицы
- •Парная и множественная регрессия
- •Линейная корреляция
- •Теорема о нормальной корреляцииEdit
- •Закон больших чисел (теорема Чебышева)
- •Неравенство Чебышева в теории вероятностей
- •Формулировки
- •Теорема Чебышева
- •Теорема Бернулли
- •Формулировка
- •Средние величины и показатели вариации
- •Выборочный метод
- •Сущность метода
- •Определение
- •Определения
- •Этапы проверки статистических гипотез
Функция распределения случайной величины
В общем случае распределение случайных величин описывается в терминах функций распределений.
Определение 3.5 Функцией
распределения случайной
величины ![]() называется
функция
называется
функция![]() ,
определяемая следующим образом
,
определяемая следующим образом
![]()
Приращения функции распределения имеют очень простой смысл:
|
(16) |
Предложение 3.1 Имеют место следующие общие свойства функций распределения:
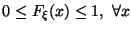 .
.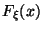 --
неубывающая функция:
--
неубывающая функция:
![]() если
если ![]()
Пределы на бесконечности
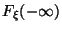
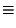
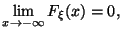
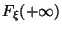
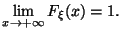
Функция непрерывна справа в каждой точке:
![]()
Мы
не будем останавливаться на доказательстве
этого предложения. Скажем лишь, что
некоторые его пункты практически
очевидны, другие несложно выводятся из
определений ![]() 3.1.
3.1.
Упражнение 3.2
Показать, что у функции распределения в каждой точке существует предел слева, т.е. существует
![]()
Упражнение 3.3
Показать, что множество точек разрыва
функции
не
более, чем счетно. (Точка разрыва: ![]() .)
.)
Пример 3.1
Простейший случай -- константа: ![]() .
В этом случае
.
В этом случае
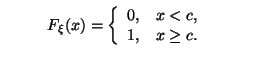
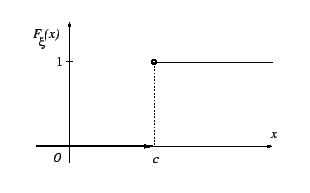
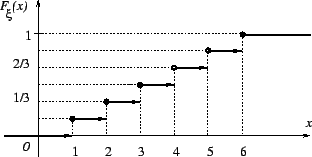
Пример 3.2
Дискретная случайная величина -- число выпавших очков на игральной кости:
25 26
Плотность вероятности
Пусть ![]() является
вероятностной мерой на
является
вероятностной мерой на ![]() ,
то есть определено вероятностное
пространство
,
то есть определено вероятностное
пространство ![]() ,
где
,
где ![]() обозначает борелевскую
σ-алгебру на
.
Пусть
обозначает борелевскую
σ-алгебру на
.
Пусть ![]() обозначает меру
Лебега на
.
обозначает меру
Лебега на
.
Определение
1. Вероятность
называется абсолютно
непрерывной (относительно
меры Лебега) (![]() ),
если любое борелевское множество нулевой
меры Лебега также имеет вероятность
ноль:
),
если любое борелевское множество нулевой
меры Лебега также имеет вероятность
ноль:
![]()
Если
вероятность
абсолютно
непрерывна, то согласно теореме
Радона-Никодима существует
неотрицательная борелевская
функция ![]() такая,
что
такая,
что
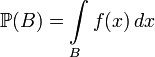 ,
,
где
использовано общепринятое сокращение ![]() ,
и интеграл понимается в
смысле Лебега.
,
и интеграл понимается в
смысле Лебега.
Определение
2. В
более общем виде, пусть ![]() —
произвольное измеримое
пространство,
а
—
произвольное измеримое
пространство,
а ![]() и
и ![]() —
две меры на
этом пространстве. Если найдется
неотрицательная
—
две меры на
этом пространстве. Если найдется
неотрицательная ![]() ,
позволяющая выразить меру
через
меру
в
виде
,
позволяющая выразить меру
через
меру
в
виде
![]()
то такую функцию называют плотностью меры по мере , или производной Радона-Никодима меры относительно меры , и обозначают
![]() .
.
[Править]Свойства плотности вероятности
Плотность вероятности определена почти всюду. Если является плотностью вероятности и
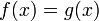 почти
всюду относительно меры Лебега, то и
функция
почти
всюду относительно меры Лебега, то и
функция 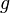 также
является плотностью вероятности
.
также
является плотностью вероятности
.
Интеграл от плотности по всему пространству равен единице:
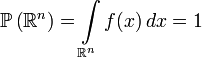 .
.
Обратно,
если ![]() —
неотрицательная п.в. функция, такая
что
—
неотрицательная п.в. функция, такая
что 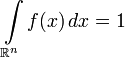 ,
то существует абсолютно непрерывная
вероятностная мера
на
такая,
что
является
её плотностью.
,
то существует абсолютно непрерывная
вероятностная мера
на
такая,
что
является
её плотностью.
Замена меры в интеграле Лебега:
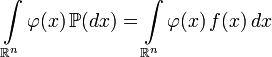 ,
,
где ![]() любая
борелевская функция, интегрируемая
относительно вероятностной меры
.
любая
борелевская функция, интегрируемая
относительно вероятностной меры
.
27
Числовые характеристики случайных величин
Математическое ожидание. Математическим ожиданием дискретной случайной величины Х , принимающей конечное число значений хi с вероятностями рi , называется сумма:
![]() (6а)
(6а)
Математическим ожиданием непрерывной случайной величины Х называется интеграл от произведения ее значений х на плотность распределения вероятностей f(x):
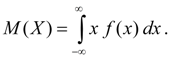 (6б)
(6б)
Несобственный интеграл (6б) предполагается абсолютно сходящимся (в противном случае говорят, что математическое ожидание М ( Х) не существует). Математическое ожидание характеризует среднее значение случайной величины Х. Его размерность совпадает с размерностью случайной величины.
Свойства математического ожидания:
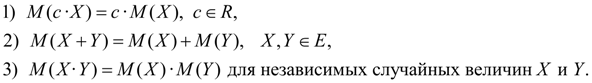 (7)
(7)
Дисперсия. Дисперсией случайной величины Х называется число:
![]() (8)
(8)
Дисперсия является характеристикой рассеяния значений случайной величины Х относительно ее среднего значения М ( Х ). Размерность дисперсии равна размерности случайной величины в квадрате. Исходя из определений дисперсии (8) и математического ожидания (5) для дискретной случайной величины и (6) для непрерывной случайной величины получим аналогичные выражения для дисперсии:
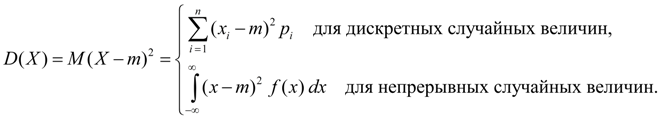 (9)
(9)
Здесь m = М ( Х ).
Свойства дисперсии:
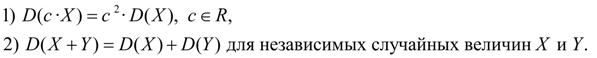 (10)
(10)
Среднее квадратичное отклонение:
![]() (11)
(11)
Так как размерность среднего квадратичного отклонения та же, что и у случайной величины, оно чаще, чем дисперсия, используется как мера рассеяния.
Моменты распределения. Понятия математического ожидания и дисперсии являются частными случаями более общего понятия для числовых характеристик случайных величин – моментов распределения. Моменты распределения случайной величины вводятся как математические ожидания некоторых простейших функций от случайной величины. Так, моментом порядка k относительно точки х0называется математическое ожидание М ( Х – х0)k . Моменты относительно начала координат х = 0 называются начальными моментамии обозначаются:
![]() (12)
(12)
Начальный момент первого порядка есть центр распределения рассматриваемой случайной величины:
![]() (13)
(13)
Моменты относительно центра распределения х = m называются центральными моментами и обозначаются:
![]() (14)
(14)
Из (7) следует, что центральный момент первого порядка всегда равен нулю:
![]() (15)
(15)
Центральные моменты не зависят от начала отсчета значений случайной величины, так как при сдвиге на постоянное значение С ее центр распределения сдвигается на то же значение С, а отклонение от центра не меняется: Х – m = (Х – С) – (m – С). Теперь очевидно, что дисперсия – это центральный момент второго порядка:
![]() (16)
(16)
Асимметрия. Центральный момент третьего порядка:
![]() (17)
(17)
служит для оценки асимметрии распределения. Если распределение симметрично относительно точки х = m, то центральный момент третьего порядка будет равен нулю (как и все центральные моменты нечетных порядков). Поэтому, если центральный момент третьего порядка отличен от нуля, то распределение не может быть симметричным. Величину асимметрии оценивают с помощью безразмерногокоэффициента асимметрии:
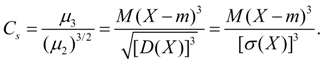 (18)
(18)
Знак коэффициента асимметрии (18) указывает на правостороннюю или левостороннюю асимметрию (рис. 2).
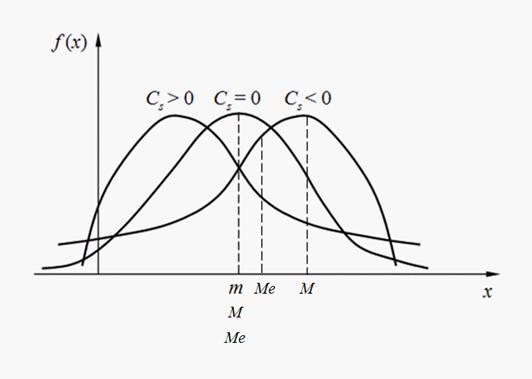 Рис.
2. Виды асимметрии распределений.
Рис.
2. Виды асимметрии распределений.
Эксцесс. Центральный момент четвертого порядка:
![]() (19)
(19)
служит
для оценки так называемого эксцесса,
определяющего степень крутости
(островершинности) кривой распределения
вблизи центра распределения по отношению
к кривой нормального распределения.
Так как для нормального распределения![]() ,
то в качестве эксцесса принимается
величина:
,
то в качестве эксцесса принимается
величина:
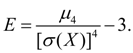 (20)
(20)
На рис. 3 приведены примеры кривых распределения с различными значениями эксцесса. Для нормального распределения Е = 0. Кривые, более островершинные, чем нормальная, имеют положительный эксцесс, более плосковершинные – отрицательный.
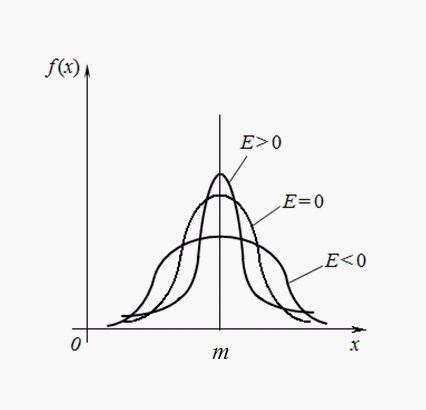 Рис.
3. Кривые распределения с различной
степенью крутости (эксцессом).
Рис.
3. Кривые распределения с различной
степенью крутости (эксцессом).
Моменты более высоких порядков в инженерных приложениях математической статистики обычно не применяются.
Мода дискретной случайной величины – это ее наиболее вероятное значение. Модой непрерывной случайной величиныназывается ее значение, при котором плотность вероятности максимальна (рис. 2). Если кривая распределения имеет один максимум, то распределение называется унимодальным. Если кривая распределения имеет более одного максимума, то распределение называетсяполимодальным. Иногда встречаются распределения, кривые которых имеют не максимум, а минимум. Такие распределения называютсяантимодальными. В общем случае мода и математическое ожидание случайной величины не совпадают. В частном случае, длямодального, т.е. имеющего моду, симметричного распределения и при условии, что существует математическое ожидание, последнее совпадает с модой и центром симметрии распределения.
Медиана случайной
величины Х –
это ее значение Ме ,
для которого имеет место равенство: ![]() т.е.
равновероятно, что случайная
величина Х окажется
меньше или больше Ме.
Геометрически медиана –
это абсцисса точки, в которой площадь
под кривой распределения делится пополам
(рис. 2). В случае симметричного
модального распределения медиана, мода
и математическое ожидание совпадают.
т.е.
равновероятно, что случайная
величина Х окажется
меньше или больше Ме.
Геометрически медиана –
это абсцисса точки, в которой площадь
под кривой распределения делится пополам
(рис. 2). В случае симметричного
модального распределения медиана, мода
и математическое ожидание совпадают.
28
Нормальным называется
распределение вероятностей непрерывной
случайной величины, которое описывается
плотностью вероятности
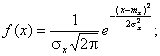
Нормальное распределение |
Распределение вероятностей переменной случайной величины Х, имеющее плотность вероятности
где
Нормальная кривая распределения. Если говорят о распределении ошибок, приведенная выше функция называется нормальным законом ошибок, а кривая распределения — нормальной кривой ошибок. |